热身训练1 Game

http://acm.hdu.edu.cn/showproblem.php?pid=5242

简要题意：

一棵树有n个节点，每个节点x有一个权值wi，我们要从根节点出发(不可回头)，去收集每个节点的权值，值得注意的是，每个权值只会被收集一次。求最多可得的值

分析：

我们肯定从根节点开始走，一直走到一个尚未走过的叶子节点

用树形dp可以轻松知道，以x为根的子树，一次最多能产生的贡献

贪心的角度来做，我们每次肯定都走贡献最大的路径

于是我们用一个优先队列，记录住每个节点的最大贡献以外的贡献

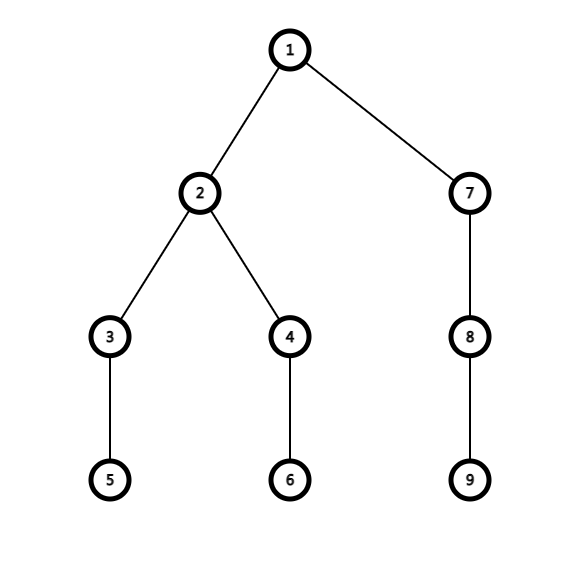
这是我们原有的树

假如说，1~5这条路径权值最大

我们走完1~5后，树会变成这样

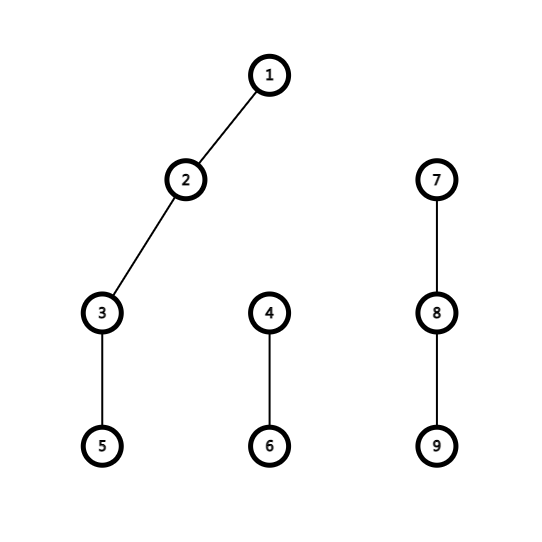
我们接下来要得到贡献，一定是从4~5或者7~8当中选取最长者(所以将他俩放入大根堆里面，就可以轻松加愉快滴解决问题了！！！)

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define int long long
const int N=2e5, M=4e5;
priority_queue<int>Q;
int tt, las[N], ed[M], nt[M], f[N], val[N];
inline void add(const int x, const int y)
{
    ed[++tt]=y; nt[tt]=las[x]; las[x]=tt;
}
void DFS(const int x, const int fa)
{
    int mx=0;
    for(re i=las[x];i;i=nt[i])
    {
        int v=ed[i];
        if(v != fa)
        {
            DFS(v, x);
            mx = max(mx, f[v]);
        }
    }
    f[x] = val[x] + mx; // 得到x为根的子树所能得到的最大值
    for(re i=las[x];i;i=nt[i])
    {
        int v=ed[i];
        if(v != fa && mx != f[v]) Q.push(f[v]); // 将非最大的放入大根堆
    }
}
signed main()
{
    int T, n, k;
    scanf("%lld",&T);
    for(re h=1;h<=T;++h)
    {
        memset(las, 0, sizeof(las)); tt=0;
        scanf("%lld%lld",&n,&k);
        for(re i=1;i<=n;++i)
        {
            scanf("%lld",&val[i]);
        }
        for(re i=1;i<n;++i)
        {
            int x, y;
            scanf("%lld%lld",&x,&y);
            add(x, y);
            add(y, x);
        }
        DFS(1, 0);
        int ans=0;
        ans += f[1]; // 先加上最长的一条
        while(--k && !Q.empty()) // 大根堆取前k-1个
        {
            ans += Q.top();
            Q.pop();
        }
        while(!Q.empty()) Q.pop();
        printf("Case #%lld: %lld\n", h, ans);
    }
}

made by kzsn

“我和我最后的倔强，握紧双手绝对不放”

“下一站是不是天堂，就算失望，不能绝望” ----《倔强》五月天