Coursera Deep Learning笔记 改善深层神经网络：超参数调试 正则化以及梯度相关

笔记：Andrew Ng's Deeping Learning视频

参考：https://xienaoban.github.io/posts/41302.html

参考：https://blog.csdn.net/u012328159/article/details/80210363

1. 训练集、验证集、测试集(Train, Dev, Test Sets)

• 当数据量小的时候, 70% 训练, 30% 测试；或 60% 训练、20% 验证、20%测试.

  • 训练集( training set)：用来训练模型，即被用来 学习 得到系统的 参数取值.

  • 测试集( testing set)：用于最终报告模型的评价结果，因此在训练阶段测试集中的样本应该是不可见的.

  • 对训练集做进一步划分为 训练集、验证集 validation set.

    • 验证集：与测试集类似，也是用于评估模型的性能.

    • 区别：是 验证集 主要 用于 模型选择 和 调整超参数，因而一般不用于报告最终结果.

• 当我们有大于100万条数据时, 测试集验证集各取1万条即可, 足以评估单个分类器.

• 确保验证集和测试集的数据来自同一分布.

• 如果不需要无偏估计, 可以不设置测试集; 当没设立测试集的时候, 验证集通常被人们称为测试集.

2. 偏差、方差(Bias, Variance)

• 高偏差(high bias)称为"欠拟合"(underfitting), 训练集误差与验证集误差都高.

  • 选择一个新的网络，比如含有更多隐藏层或者隐藏单元的网络，或者花费更多时间来训练网络，或者尝试更先进的优化算法【后面深入讲解】

• 高方差(high variance)称为"过拟合"(overfitting), 训练集误差很低，而验证集误差很高.

  • 解决方法是 正则化

  • 准备更多的数据.

3. 正则化(Regularization)

• 避免过拟合
• 减少网络误差

3.1 逻辑回归中的L1正则化, L2正则化

对于L1正则化, 为代价函数添加L1范数:(几乎不用了)

\[J(w, b) = \frac{1}{m} \sum^{m}_{i=1} \mathcal{L}(a^{(i)}, y^{(i)}) + \frac{\lambda}{2m} ||w||_1
\]

其中：

\[||w||_1 = \sum^{n_x}_{j=1} |w_j|
\]

• 使用L1正则化, w最终会是稀疏的(w中含很多0), 有利于压缩模型
• 但也没有降低太多内存, 所以不能将压缩作为L1正则化的目的。通常我们使用L2正则化.

---

对于L2正则化, 为代价函数添加L2范数:

\[J(w, b) = \frac{1}{m} \sum^{m}_{i=1} \mathcal{L}(a^{(i)}, y^{(i)}) + \frac{\lambda}{2m} ||w||_2^2
\]

其中：

\[||w||^2_2 = \sum^{n_x}_{j=1} w_j^2 = w^Tw
\]

尽管 \(b\) 也是参数, 但我们没有必要添加 \(\frac{\lambda}{2m}b^2\) 项， 因为 \(w\) 几乎涵盖了所有参数, 而 \(b\) 只是众多参数中的一个, 可以忽略不计(当然加上也没问题).

3.2 神经网络中的L2正则化

对于神经网络L2正则化(权重衰减)，为代价函数添加L2范数：

\[J(w, b) = \frac{1}{m} \sum^{m}_{i=1} \mathcal{L}(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^{L}||w||_F^2
\]

其中，弗罗贝尼乌斯范数(即矩阵L2范数,矩阵中所有元素平方和):

\[||w^{[l]}||_F^2 = \sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}} (w_{ij}^{[l]})^2 \\
注: W: (n^{[l]}, n^{[l-1]})
\]

则在反向传播时,

\[\begin{aligned}
dw^{[l]} & = (\text{from backprop}) + \frac{\lambda}{m}w^{[l]} \\
w^{[l]} & = w^{[l]} -\alpha dw^{[l]} \\
\end{aligned}
\]

正则项说明, 无论 \(w^{[l]}\) 是什么, 我们都努力使之更小(趋于0)， 则计算得的 \(z^{[l]}=w^{[l]}a^{[l−1]}+b^{[l]}\) 此时也更小

\(z^{[l]}\) 更容易(以tanh例) 落在激活函数 \(g(z^{[l]})\) 中间那一段接近线性的部分, 以达到简化网络的目的

• 注：线性的激活函数使得无论多少层的网络, 效果都和一层一样

3.3 随机失活(Dropout)正则化

对每一轮的训练, Dropout 遍历网络的每一层, 设置神经网络中每一层每个节点的失活概率

被随机选中失活的节点临时被消除, 不参与本轮的训练, 于是得到一个更小的网络.

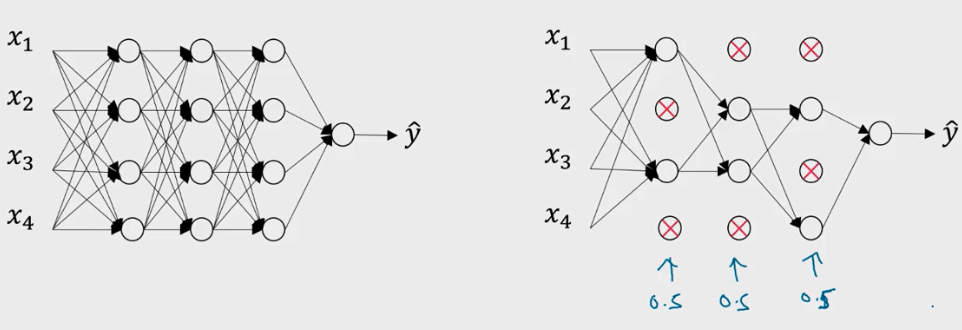
最常用的为反向随机失活(Inverted Dropout).

• 该方法在向前传播时, 根据随机失活的概率 (例如0.2)，将每一层(例如 \(l\) 层)的 \(a^{[l]}\) 矩阵(a=g(z)) 中被选中失活的元素置为0， 则该层的 \(a^{[l]}\) 相当于少了 20% 的元素.

• 为了不影响下一层 \(z^{[l+1]}\) 的期望值, 我们需要 \(a^{[l]}\) /= 0.8 以修正权重.

代码实现：

• 前向传播

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.8):
    """
    X -- input dataset, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2",...,"WL", "bL"
                    W -- weight matrix of shape (size of current layer, size of previous layer)
                    b -- bias vector of shape (size of current layer,1)
    keep_prob: probability of keeping a neuron active during drop-out, scalar
    :return:
    AL: the output of the last Layer(y_predict)
    caches: list, every element is a tuple:(W,b,z,A_pre)
    """
    np.random.seed(1)  #random seed
    L = len(parameters) // 2            # number of layer
    A = X
    caches = [(None,None,None,X,None)]  # 用于存储每一层的，w,b,z,A,D第0层w,b,z用none代替
    # calculate from 1 to L-1 layer
    for l in range(1, L):
        A_pre = A
        W = parameters["W" + str(l)]
        b = parameters["b" + str(l)]
        z = np.dot(W, A_pre) + b  # 计算z = wx + b
        A = relu(z)  # relu activation function
        D = np.random.rand(A.shape[0], A.shape[1]) #initialize matrix D
        D = (D < keep_prob)       #convert entries of D to 0 or 1 (using keep_prob as the threshold)
        A = np.multiply(A, D)     #shut down some neurons of A
        A = A / keep_prob         # scale the value of neurons that haven't been shut down
        caches.append((W, b, z, A,D))
    # calculate Lth layer
    WL = parameters["W" + str(L)]
    bL = parameters["b" + str(L)]
    zL = np.dot(WL, A) + bL
    AL = sigmoid(zL)
    caches.append((WL, bL, zL, A))
    return AL, caches

• 后向传播

def backward_propagation_with_dropout(AL, Y, caches, keep_prob = 0.8):
    """
        Implement the backward propagation presented in figure 2.
        Arguments:
        X -- input dataset, of shape (input size, number of examples)
        Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
        caches -- caches output from forward_propagation(),(W,b,z,pre_A)
        keep_prob: probability of keeping a neuron active during drop-out, scalar
        Returns:
        gradients -- A dictionary with the gradients with respect to dW,db
        """
    m = Y.shape[1]
    L = len(caches) - 1
    # print("L:   " + str(L))
    # calculate the Lth layer gradients
    prev_AL = caches[L - 1][3]
    dzL = 1. / m * (AL - Y)
    dWL = np.dot(dzL, prev_AL.T)
    dbL = np.sum(dzL, axis=1, keepdims=True)
    gradients = {"dW" + str(L): dWL, "db" + str(L): dbL}
    # calculate from L-1 to 1 layer gradients
    for l in reversed(range(1, L)): # L-1,L-2,...,1
        post_W = caches[l + 1][0]  # 要用后一层的W
        dz = dzL  # 用后一层的dz
        dal = np.dot(post_W.T, dz)
        Dl = caches[l][4] #当前层的D
        dal = np.multiply(dal, Dl) #Apply mask Dl to shut down the same neurons as during the forward propagation
        dal = dal / keep_prob #Scale the value of neurons that haven't been shut down
        Al = caches[l][3]  #当前层的A
        dzl = np.multiply(dal, relu_backward(Al))#也可以用dzl=np.multiply(dal, np.int64(Al > 0))来实现
        prev_A = caches[l-1][3]  # 前一层的A
        dWl = np.dot(dzl, prev_A.T)
        dbl = np.sum(dzl, axis=1, keepdims=True)

        gradients["dW" + str(l)] = dWl
        gradients["db" + str(l)] = dbl
        dzL = dzl  # 更新dz
    return gradients

注意：

• 训练时的 "\(a^{[l]}\) /= 0.8" 要修复权重

• 在测试阶段无需使用 Dropout.(测试阶段要关掉)

• Dropout 不能与梯度检验同时使用，因为 Dropout 在梯度下降上的代价函数J难以计算.

3.4 其他正则化

数据扩增:

• 比如训练分类猫咪的图片, 将图片左右翻转、旋转一个小角度、稍微变形处理等, 可以人工合成数据.

Early Stopping:

• 运行梯度下降时, 我们可以绘制训练误差, 当验证集误差不降反增的时候, 停止训练.

• 缺点：是可能导致代价J值不够小, 却又没解决继续训练可能导致的过拟合问题.

4. 归一化(Normalizing)

• 加速训练

输入的归一化有两个步骤:

1. 均值调整为0
2. 方差归一化

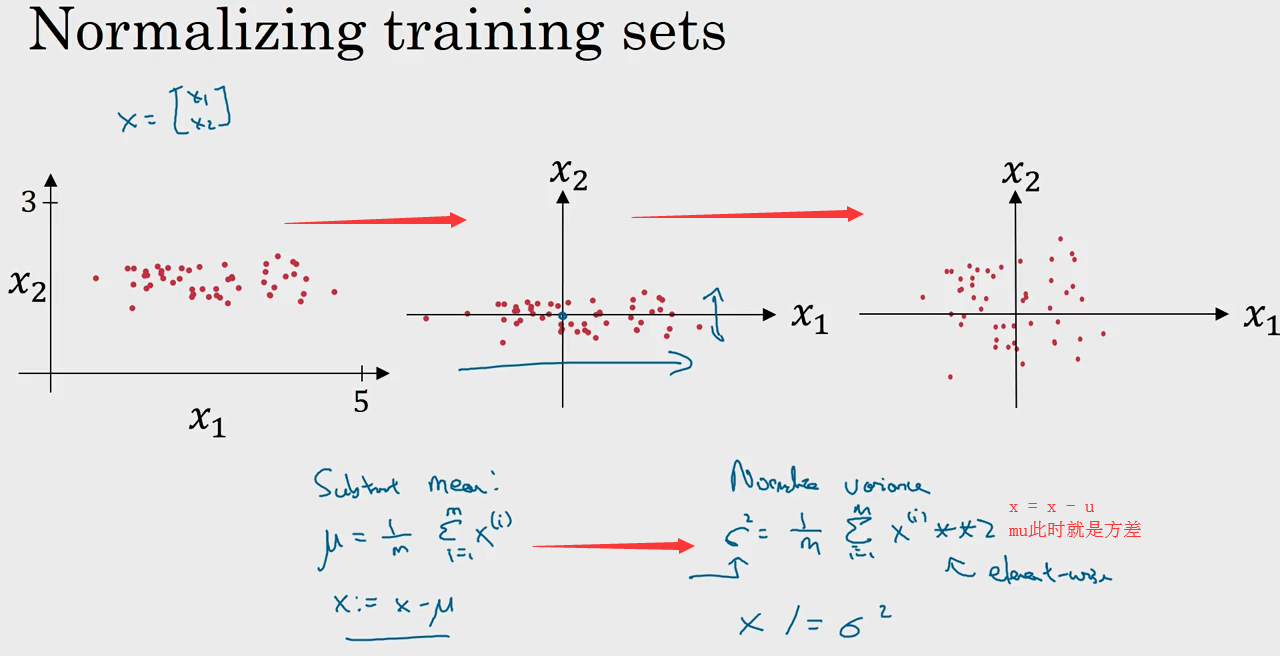
注：此时x1, x2方差均为1

归一化直观的理解就是使得代价函数更圆, 更容易优化代价函数.

5. 梯度消失/爆炸(Vanishing / Exploding Gradients)

• 加速训练

为了方便理解，假设使用了线性激活函数 g(z)=z , 且

\[W=W^{[L-1]}=...=W^{[2]}=W^{[1]}
\]

则：

\[\begin{aligned}
\hat{y} & = W^{[L]}W^{[L-1]}...W^{[2]}W^{[1]}x \\
& = W^{[L]}W^{L-1}x
\end{aligned}
\]

可知若 \(W\) 中有元素权重为 1.5 , 则最终得到 \({1.5}^{L−1}\) 若层数很深, 计算得 \(\hat{y}\) 也很大;

同理若权重为 0.5 , 进行 L−1 次幂运算后值会很小. 这便是梯度爆炸 与 梯度消失.

---

有效的解决方案:

• 由于 \(z=w_1x_1+w_2x_2+...+w_nx_n\) (忽略 \(b\)), 为了预防 \(z\) 太大或太小, 则 \(n\) 越大时, 期望 \(w_i\) 越小

• 则在随机(0~1)初始化 \(W\) 时, 我们对其乘上一个小于1的倍数, 使之更小.

  • 对于Tanh, 权重乘上 \(\sqrt{\frac{1}{n^{[l-1]}}}\) 或者 \(\sqrt{\frac{2}{n^{[l-1]}+n^{[l]}}}\)

  • 对于Relu, 权重乘上 \(\sqrt{\frac{2}{n^{[l-1]}}}\)

# GRADED FUNCTION: initialize_parameters_he

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """

    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers

    for l in range(1, L + 1):
        ### START CODE HERE ### (≈ 2 lines of code)
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * (np.sqrt(2. / layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
        ### END CODE HERE ###

    return parameters

随机用大的数进行初始化W，画出的cost下降的曲线：

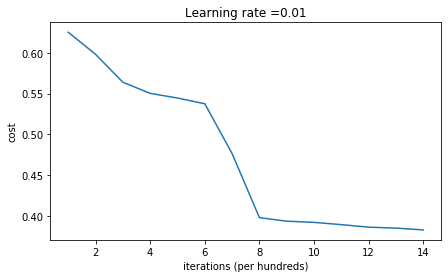
用上面方法进行初始化W，画出的cost下降的曲线：

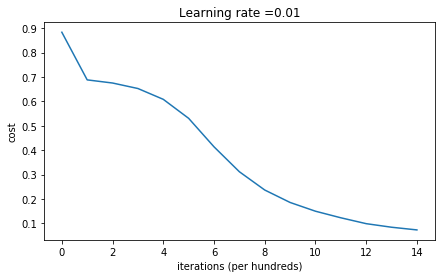
6. 梯度检验

在反向传播的时候, 如果怕自己 \(d\theta[i] = \frac{\partial J}{\partial \theta_i}\) 等算错, 可以用导数的定义, 计算

\({for\ each\ i:}\)

\[d\theta_{approx}[i] = \frac{J(\theta_1, \theta_2, ..., \theta_i + \varepsilon, ...) - J(\theta_1, \theta_2, ..., \theta_i - \varepsilon, ...)}{2\varepsilon}
\]

然后根据 两者误差 估计自己是否算错. 该方法仅用来调试

\[Check: \frac{||d\theta_{approx} - d\theta||_2}{||d\theta_{approx}||_2 + ||d\theta||_2} \approx 10^{-7}
\]

且不能同 Dropout 同时使用.