你管这破玩意叫CPU？

每次回家开灯时你有没有想过，用你按的开关实际上能打造出 复杂的 CPU来，只不过需要的数量可能比较多，也就几十亿个吧。

伟大的发明

过去200年人类最重要的发明是什么？蒸汽机？电灯？火箭？这些可能都不是，最重要的也许是这个小东西：

这个小东西就叫晶体管，你可能会问，晶体管有什么用呢？

实际上晶体管的功能简单到不能再简单，给一端通上电，那么电流可以从另外两端通过，否则不能通过，其本质就是一个开关。

就是这个小东西的发明让三个人获得了诺贝尔物理学奖，可见其举足轻重的地位。

无论程序员编写的程序多么复杂，软件承载的功能最终都是通过这个小东西简单的开闭完成的，除了神奇二字，我想不出其它词来。

AND、OR、NOT

现在有了晶体管，也就是开关，在此基础之上就可以搭积木了，你随手搭建出来这样三种组合：

• 两个开关只有同时打开电流才会通过，灯才会亮
• 两个开关中只要有一个打开电流就能通过，灯就会亮
• 当开关关闭时电流通过灯会亮，打开开关灯反而电流不能通过灯会灭

天赋异禀的你搭建的上述组合分别就是：与门，AND Gate、或门，OR gate、非门，NOT gate，用符号表示就是这样：

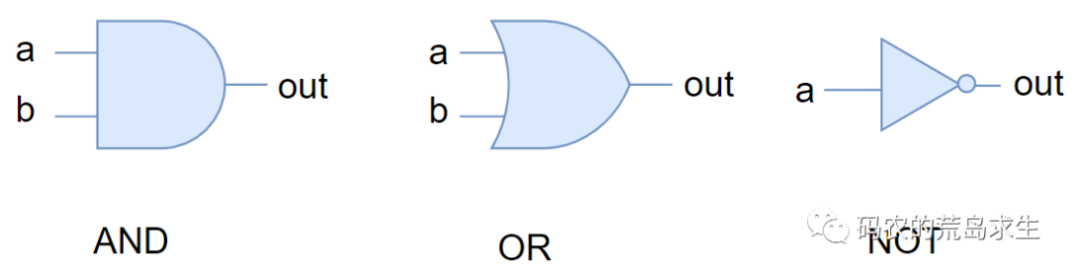
道生一、一生二、二生三、三生万物

最神奇的是，你随手搭建的三种电路竟然有一种很amazing的特性，那就是：任何一个逻辑函数最终都可以通过AND、OR以及NOT表达出来，这就是所谓的逻辑完备性，就是这么神奇。

也就是说给定足够的AND、OR以及NOT门，就可以实现任何一个逻辑函数，除此之外我们不需要任何其它类型的逻辑门电路，这时我们认为{AND、OR、NOT}就是逻辑完备的。

这一结论的得出吹响了计算机革命的号角，这个结论告诉我们计算机最终可以通过简单的{AND、OR、NOT}门构造出来，就好比基因。

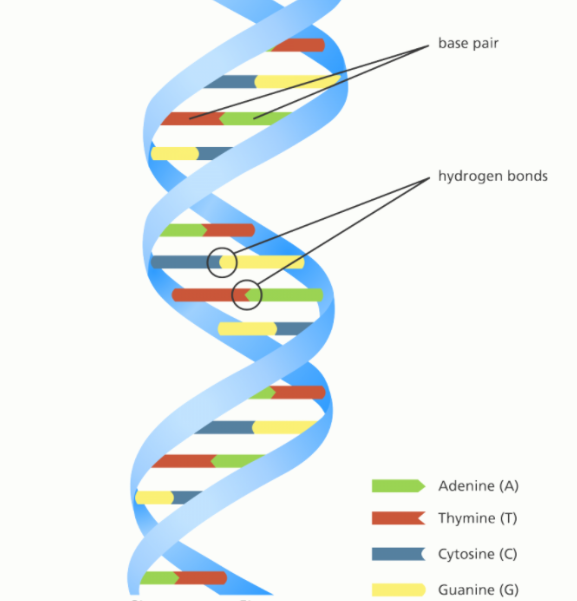
老子有云：道生一、一生二、二生三、三生万物，实乃异曲同工之妙。

虽然，我们可以用{AND、OR、NOT}来实现所有的逻辑运算，但我们真的需要把所有的逻辑运算都用{AND、OR、NOT}们实现出来吗？显然不是，而且这也不太可行。

计算能力是怎么来的

现在能生成万物的基础元素与或非门出现了，接下来我们着手设计CPU 最重要的能力：计算，以加法为例。

由于CPU只认知 0 和 1，也就是二进制，那么二进制的加法有哪些组合呢：

• 0 + 0，结果为0，进位为0
• 0 + 1，结果为1，进位为0
• 1 + 0，结果为1，进位为0
• 1 + 1，结果为0，进位为1，二进制嘛！

注意进位一列，只有当两路输入的值都是 1 时，进位才是 1 ，看一下你设计的三种组合电路，这就是与门啊，有没有！

再看下结果一列，当两路输入的值不同时结果为1，输入结果相同时结果为0，这就是异或啊，有没有！我们说过与或非门是逻辑完备可以生万物的，异或逻辑当然不在话下，用一个与门和一个异或门就可以实现二进制加法：

上述电路就是一个简单的加法器，就问你神奇不神奇，加法可以实现，其它的也一样能用与或非门实现，逻辑完备嘛。

根据需要可以将不同的算数运算设计出来，这就是所谓的arithmetic/logic unit，ALU，CPU 中专门负责运算的模块，本质上和上面的简单电路没什么区别，就是更加复杂而已。

现在，通过与或非门的组合我们获得了计算能力。

但，只有计算能力是不够的，电路需要能记得住信息。

神奇的记忆能力

到目前为止，你设计的组合电路比如加法器天生是没有办法存储信息的，它们只是简单的根据输入得出输出，但输入输出总的有个地方能够保存起来，这就是需要电路能保存信息。

电路怎么能保存信息呢？你不知道该怎么设计，这个问题解决不了你寝食难安，吃饭时在思考、走路时在思考，蹲坑时在思考，直到有一天你在梦中遇一位英国物理学家，他给了你这样一个简单但极其神奇的电路，因为这个电路有记忆功能：

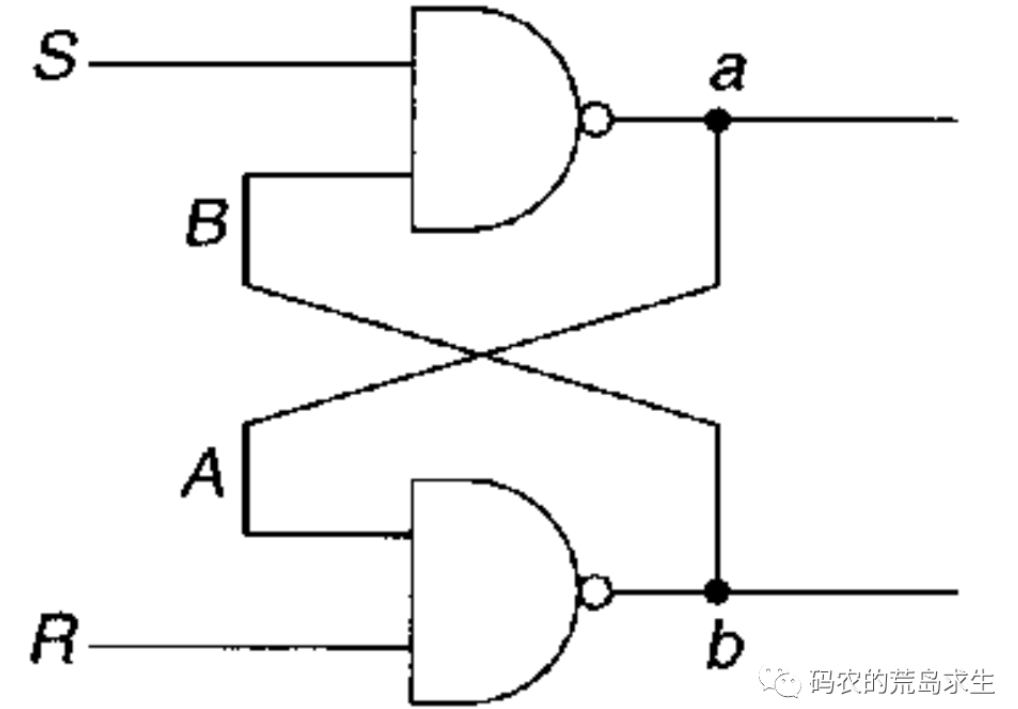
这是两个NAND门的组合，不要紧张，NAND也是有你设计的与或非门组合而成的，所谓NAND门就是与非门，先与然后取非，比如给定输入1和0，那么与运算后为0，非运算后为1，这就是与非门，这些不重要。

比较独特的是该电路的组合方式，一个NAND门的输出是两一个NAND门的输入，该电路的组合方式会生成一种很有趣的特性，只要给S和R段输入1，那么这个电路只会有两种状态:

• 要么a端为1，此时B=0、A=1、b=0；
• 要么a端为0，此时B=1、A=0、b=1;

不会再有其他可能了，我们把a端的值作为电路的输出。

此后，你把S端置为0的话(R保持为1)，那么电路的输出也就是a端永远为1，这时就可以说我们把1存到电路中了；而如果你把R段置为0的话(S保持为1)，那么此时电路的输出也就是a端永远为0，此时我们可以说把0存到电路中了。

就问你神奇不神奇，电路竟然具备存储信息的能力了。

现在为保存信息你需要同时设置S端和R端，但你的输入是有一个，为此你对电路进行了简单的改造：

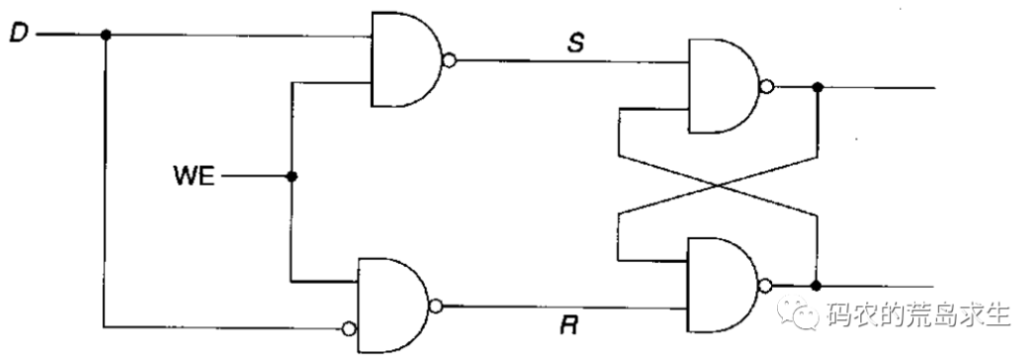
这样，当D为0时，整个电路保存的就是0，否则就是1。

寄存器与内存的诞生

现在你的电路能存储一个比特位了，想存储多个还不简单，简单的组合就可以了：

我们管这个组合电路就叫寄存器，你没有看错，我们常说的寄存器就是这个东西。

你不满足，还要继续搭建更加复杂的电路以存储更多信息，同时提供寻址功能，就这样内存也诞生了。

寄存器、内存都离不开上一节那个简单电路，只要通电，这个电路中就保存信息，但是断点后保存的信息就丢掉了，现在你应该明白为什么内存在断电后信息就丢了吧。

硬件还是软件？

现在我们可以计算、也可以存储，但现在还有一个问题，那就是尽管我们可以用{AND、OR、NOT}表达出所有的逻辑函数，但我们真的有必要把所有的逻辑运算都用与或非门实现出来吗？这显然是不现实的。

这就好比厨师，你没有听说哪个酒店的厨师专门只做一道菜吗？

最终的成品是比较复杂的，千差万别，但制作每道菜品的方式大同小异，其中包括刀工、颠勺技术等，这些是基本功，制作每道菜品都要经过这些步骤，变化的也无非就是食材、火候、调料的差异，这些放到菜谱中即可，这样给他一个菜谱他就能制作出任意的菜来，在这里厨师就好比硬件，菜谱就好比软件。

同样的道理，我们没有必要为所有的计算逻辑实现出对应的硬件，硬件只需要提供最基本的功能，最终所有的计算逻辑都通过这些最基本的功能表达出来就好，这就是所谓的软件一词的来源，硬件不可变，但软件可变，因此称为软件，不变的硬件但提供不同的软件就能让硬件提供全新的功能，无比天才的思想，人类真的是太聪明了。

同样一台计算机硬件，安装上word你就能编辑文档，安装上VS你就能写代码，安装上游戏你就能玩王者农药，硬件还是那套硬件，提供不同的软件就是实现不同的功能，每次打开电脑使用各种App时没有在内心高呼一声牛逼你都对不起计算机这么伟大的发明创造，这就是所谓的通用计算设备，这一思想是计算机科学的祖师爷图灵提出的。

扯远了，接下来我们看下硬件是怎么提供所谓的基本功能的。

硬件的基本功

让我们来思考一个问题，CPU怎么能知道自己要去对两个数进行加法计算，以及哪两个数进行加法计算呢？

很显然，你得告诉CPU，该怎么告诉呢？还记得上一节中给初始的菜谱吗？没错，CPU也需要一张菜谱告诉自己该接下来该干啥，在这里菜谱就是机器指令，指令通过我们上述实现的组合电路来执行。

接下来我们面临另一个问题，那就是这样的指令应该会很多吧，废话，还是以加法指令为例，你可以让CPU计算1+1，也可以计算1+2等等，实际上单单加法指令就可以有无数中组合，显然CPU不可能去实现所有的指令。

实际上CPU只需要提供加法操作，你提供操作数就可以了，CPU 说：“我可以打人”，你告诉CPU该打谁、CPU 说：“我可以唱歌”，你告诉CPU唱什么，CPU 说我可以做饭，你告诉CPU该做什么饭，CPU 说：“我可以炒股”，你告诉CPU快滚一边去吧韭菜。

因此我们可以看到CPU只提供机制或者说功能(打人、唱歌、炒菜，加法、减法、跳转)，我们提供策略(打谁、歌名、菜名，操作数，跳转地址)。

CPU 表达机制就通过指令集来实现的。

指令集与指令执行

指令集告诉我们 CPU 可以执行什么指令，每种指令需要提供什么样的操作数。不同类型的CPU会有不同的指令集。

指令集中的指令其实都非常简单，画风大体上是这样的：

• 从内存中读一个数，地址是abc
• 对两个数加和
• 检查一个数是不是大于6
• 把这数存储到内存，地址是abc
• 等等

看上去很像碎碎念有没有，这就是机器指令，我们用高级语言编写的程序，比如对一个数组进行排序，最终都会等价转换为上面的碎碎念指令，然后 CPU 一条一条的去执行，很神奇有没有。

接下来我们看一条可能的机器指令：

这条指令占据16比特，其中前四个比特告诉我们这是加法指令，这意味着该CPU的指令集中可以包含2^4也就是16个机器指令，这四个比特位告诉我们该指令可以做什么，剩下的bite告诉我们该怎么做，也就是把寄存器R6和寄存器R2中的值相加然后写到寄存器R6中。

可以看到，机器指令是非常繁琐的，现代程序员都使用高级语言来编写程序，关于高级程序语言以及机器指令的话题请参见《你管这破玩意叫编程语言》。

指挥家：让我们演奏一曲

现在我们的电路有了计算功能、存储功能，还可以通过指令告诉该电路执行什么操作，还有一个问题没有解决。

我们的电路有很多部分，用来计算的、用来存储的，以最简单的加法为例，假设我们要计算1+1，这两个数分别来自寄存器R1 和 R2，要知道寄存器中可以保存任意值，我们怎么能确保加法器开始工作时R1和R2中在这一时刻保存的都是1而不是其它数？

这个问题就是靠什么来协调靠什么来同步各个部分让它们协同工作呢？就像一场成功的交响乐演出是离不开指挥家，我们的计算组合电路中也需要这样一个指挥家。

负责指挥角色的就是时钟信号。

时钟信号就像指挥家手里的拿的指挥棒，指挥棒挥动一下整个乐队会整齐划一的有个相应动作，同样的，在时钟信号的每一次电压改变，整个电路中的各个寄存器(也就是整个电路的状态)会更新一下，这样我们就能确保整个电路协同工作不会这里提到的问题。

现在你应该知道CPU的主频是什么意思了吧，主频是说一秒钟指挥棒挥动了多少次，当然主频越高CPU在一秒内完成的操作也就越多。

大功告成

现在我们有了可以完成各种计算的ALU、可以存储信息的寄存器以及控制它们系统工作的时钟信号，这些就是一个极简版的CPU啦。

总结

一个小小的开关竟然能构造出功能强大的 CPU ，这背后理论和制造工艺的突破是人类史上的里程碑时刻，说 CPU 是智慧的结晶简直再正确不过。

最后，有同学问有没有书单，我也仔细回想自己认真读过的计算机数据，在这里也给出自认为很经典的几本，书单这东西贵精不贵多，我在这里精心挑选了10本 ，不要贪心，如果你真能把这里推荐的 10 本书读通，可以说你已经能超越 90% 的程序员了，详见《程序员必读经典书单》。

本文从一枚开关开始讲解了 CPU 构造的基本原理，希望这篇对大家理解 CPU 有所帮助。