普林斯顿微积分读本 大纲与重点 （by zzd）

普林斯顿微积分读本 大纲重点

由于博客园太菜，所以我用图片上传。

当前更新状态：未完待续，挖坑暂时不填了。

UPD(2018-07-08): 稍微更一下，加一个本书的某一版本下载链接：https://pan.baidu.com/s/12DWtOkB2IjmQjnpwVZ_VvA

UPD(2019-02-27):

我决定草率的更新一下。(之前的在后面……)

有些简单的结论我就不证明了。

$$\frac {d}{dx}(x^a) = ax^{a-1}$$

乘积法则：若 $h(x) = f(x) g(x) $ ，则 $h'(x) = f'(x) g(x) =f(x) g'(x) $ .

证明：

$$h'(x) = \lim_{d\rightarrow 0} \frac {f(x+d)g(x+d) -f(x)g(x)}{d}\\=\lim_{d\rightarrow 0}\frac{(f(x+d)-f(x)+f(x))(g(x+d)-g(x)+g(x))-f(x)g(x)}{d}\\=\lim_{d\rightarrow 0}\frac{(f(x+d)-f(x))g(x)+f(x)(g(x+d)-g(x))+(f(x+d)-f(x))(g(x+d)-g(x))}{d}\\=\lim_{d\rightarrow 0}\frac{f(x+d)-f(x)}{d}g(x) + \frac{g(x+d)-g(x)}d f(x)\\=f'(x) g(x) =f(x) g'(x) ​$$

商法则：若 $h(x) = \frac {f(x)}{g(x)} $ ，则 $h'(x) = \frac{f'(x)g(x) -f(x)g'(x)}{g^2(x)}$ .

证明：

$$h'(x) = \lim_{d\rightarrow 0} \cfrac{\frac{f(x+d)}{g(x+d)}-\frac{f(x)}{g(x)}}{d}\\= \lim_{d\rightarrow 0} \cfrac{\frac{f(x+d)g(x)-f(x)g(x+d)}{g(x+d)g(x)}}{d}\\= \lim_{d\rightarrow 0} \frac{(f(x+d)-f(x))g(x)-(g(x+d)-g(x))f(x)}{g(x+d)g(x)d}\\= \lim_{d\rightarrow 0}h'(x) = \frac{f'(x)g(x) -f(x)g'(x)}{g^2(x)}​$$

链式求导法则：若 $h(x) =f(g(x))$ ，则 $h'(x) = f'(g(x))g'(x)$.

证明：

$$h'(x) = \lim_{d\rightarrow 0} \frac{f(g(x+d))-f(g(x))}{d}\\=\lim_{d\rightarrow 0} \frac{(f(g(x))+f'(g(x))(g(x+d)-g(x)))-f(g(x))}{d}\\=\lim_{d\rightarrow 0} \frac{f'(g(x))(g(x+d)-g(x))}{d}\\=f'(g(x))g'(x)$$

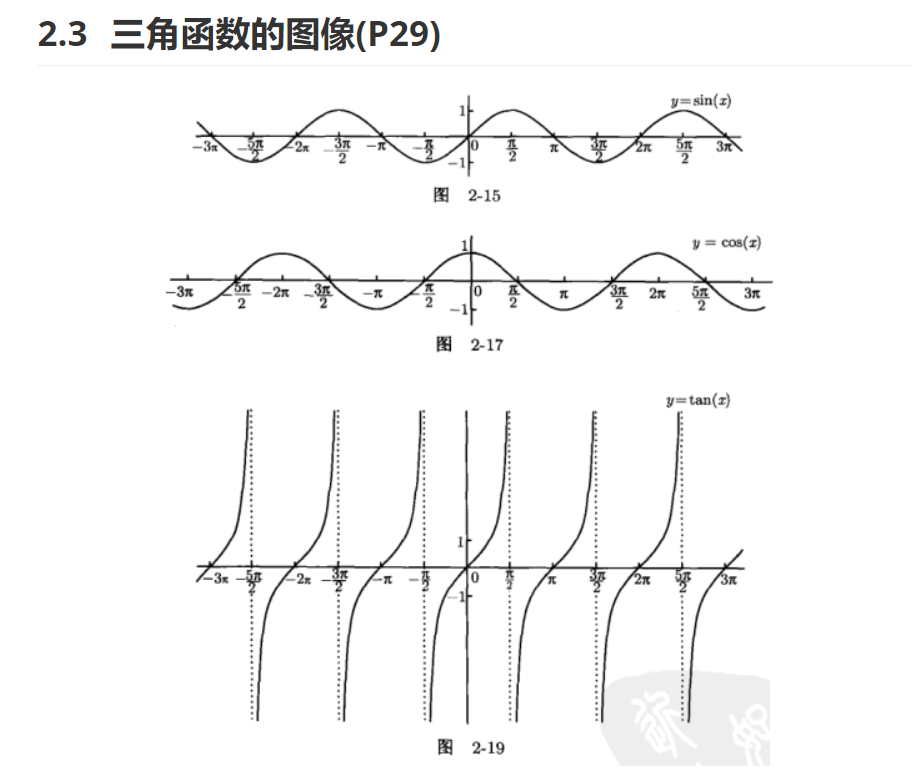
三角函数相关

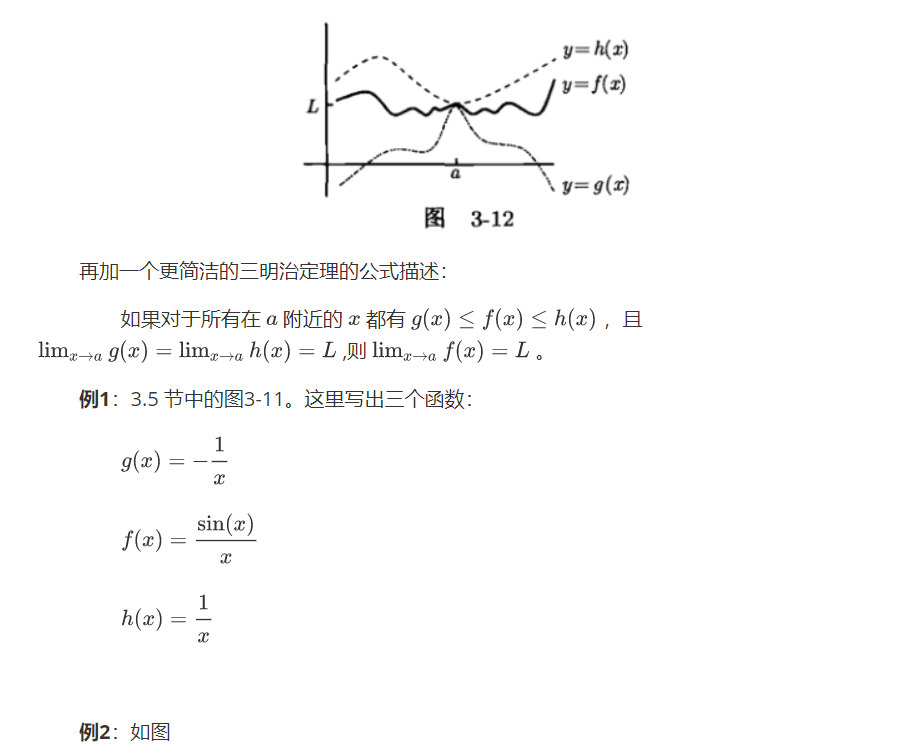
$$\lim_{x\rightarrow0}\frac{\sin(x)}{x}=1$$

证明：

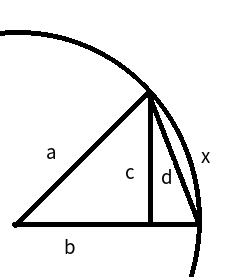
首先画个单位圆(半径为1的圆)，在上面画个三角形，设x是那个圆心角的弧度（数值上也等于对应的圆弧的长度），现在我们看看 $sin(x)$ 是什么：

$sin(x) = c/a = c$

当 $x$ 趋于0的时候，$c/d$ 和 $d/x$ 都趋于 1 ，所以 $c/x = (c/d)/(d/x)$ 也趋于1 ，所以这个结论得证。

$$\lim_{x\rightarrow0}\frac{1-\cos(x)}{x}=0​$$

证明：

$$\lim_{x\rightarrow0}\frac{1-\cos(x)}{x} = \lim_{x\rightarrow0}\frac{(1-\cos(x))(1+\cos(x))}{x}\cdot \frac{1}{1+\cos(x)}\\=\lim_{x\rightarrow0}\frac{\sin^2(x)}{x}\cdot 0.5\\=0$$

$$\sin'(x) = \cos(x)$$

证明：

$$\sin'(x) = \lim_{d\rightarrow 0 }\frac{\sin(x+d) -\sin(x)}{d} \\= \lim_{d\rightarrow 0 }\frac{\sin(x)\cos(d)+\sin(d)\cos(x)-\sin(x)}{d}\\= \lim_{d\rightarrow 0 } \frac{\sin(x)(1-\cos(d))+\cos(x)\sin(d)}{d}\\=\lim_{x\rightarrow0}0+\cos(x)\\=\cos(x)​$$

类似的证明方法可得：

$$\cos'(x) =-\sin(x)$$

$$\tan'(x) = \sec^2(x)$$

$$\sec'(x) = \sec(x)\tan(x)$$

$$\csc'(x) = -\csc(x)\cot(x) $$

$$\cot'(x) = -\csc^2(x)$$

定义：

$$e^r= \lim_{h\rightarrow 0^+}((1+h)^{1/h})^r = \lim_{n\rightarrow \infty}(1+\frac rn )^n$$

$$\ln(x) = \log _e(x)$$

$$\ln'(x) = \frac 1 x $$

证明：

$$\ln'(x) = \lim_{d\rightarrow 0 }\frac{\ln(x+d)-\ln(x)}{d}\\=\lim_{d\rightarrow 0 }\frac{1}{d}\ln\left(\frac{x+d}{x}\right)\\=\lim_{d\rightarrow 0 }\ln\left(1+\frac{d}{x}\right)^{1/d}\\=\lim_{d\rightarrow 0 }\ln e^{1/x} \\= \frac 1 x $$

$$\log'_a(x) = \frac 1 {x\ln(b)}$$

$$\frac {\rm d} {{\rm d}x} (e^x ) = e^x ​$$

证明：

$$\frac{{\rm d}(\ln(x))}{{\rm d}y} = \frac{1}{y}$$

$$\frac{{\rm d}y}{{\rm d}(\ln(x))} = y$$

$$\frac{{\rm d}(e^{\ln(x)})}{{\rm d}(\ln(x))} = e^{\ln(x)}$$

所以

$$\frac {\rm d} {{\rm d}x} (e^x ) = e^x $$

洛必达法则

对 $f(x)$ 求不定积分就是求一个函数 $g(x)$ 满足 $g'(x)=f(x)​$ 。

$$\begin{array} { l } { \frac { \mathrm { d } } { \mathrm { d } x } x ^ { a } = a x ^ { a - 1 } } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \ln ( x ) = \frac { 1 } { x } } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \mathrm { e } ^ { x } = \mathrm { e } ^ { x } } \\ { \frac { \mathrm { d } } { \mathrm { d } x } b ^ { x } = b ^ { x } \ln ( b ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \sin ( x ) = \cos ( x ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \cos ( x ) = - \sin ( x ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \tan ( x ) = \sec ^ { 2 } ( x ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \sec ( x ) = \sec ( x ) \tan ( x ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \cot ( x ) = - \csc ^ { 2 } ( x ) } \\ { \frac { \mathrm { d } } { \mathrm { d } x } \csc ( x ) = - \csc ( x ) \cot ( x ) } \\ { \frac { \mathrm { d } x } { \mathrm { d } x } \sin ^ { - 1 } ( x ) = \frac { 1 } { \sqrt { 1 - x ^ { 2 } } } } \\ { \frac { \mathrm { d } x } { \mathrm { d } x } \tan ^ { - 1 } ( x ) = \frac { 1 } { 1 + x ^ { 2 } } } \\ { \frac { \mathrm { d } x } { \mathrm { d } x } \sec ^ { - 1 } ( x ) = \frac { 1 } { | x | \sqrt { x ^ { 2 } - 1 } } } \\ { \frac { \mathrm { d } x } { \mathrm { d } x } \sinh ( x ) = \cosh ( x ) } \\ { \frac { \mathrm { d } x } { \mathrm { d } x } \cosh ( x ) = \sinh ( x ) } \\ { \int x ^ { a } \mathrm { d } x = \frac { x ^ { a + 1 } } { a + 1 } + C \quad ( \text { if } a \neq - 1 ) } \\ { \int \frac { 1 } { x } \mathrm { d } x = \ln | x | + C } \\ { \int \mathrm { e } ^ { x } \mathrm { d } x = \mathrm { e } ^ { x } + C } \\ { \int b ^ { x } \mathrm { d } x = \frac { b ^ { x } } { \ln ( b ) } + C } \\ {\int \cos ( x ) \mathrm { d } x = \sin ( x ) + C } \\ { \int \sin ( x ) \mathrm { d } x = - \cos ( x ) + C } \\ { \int \sec ^ { 2 } ( x ) \mathrm { d } x = \tan ( x ) + C } \\ { \int \sec ( x ) \tan ( x ) \mathrm { d } x = \sec ( x ) + C } \\ { \int \csc ^ { 2 } ( x ) \mathrm { d } x = - \cot ( x ) + C }\\{ \int \csc ( x ) \cot ( x ) \mathrm { d } x = - \csc ( x ) + C } \\ { \int \frac { 1 } { \sqrt { 1 - x ^ { 2 } } } \mathrm { d } x = \sin ^ { - 1 } ( x ) + C } \\ { \int \frac { 1 } { 1 + x ^ { 2 } } \mathrm { d } x = \tan ^ { - 1 } ( x ) + C } \\ { \int \frac { 1 } { | x | \sqrt { x ^ { 2 } - 1 } } \mathrm { d } x = \sec ^ { - 1 } ( x ) + C } \\ { \int \cosh ( x ) \mathrm { d } x = \sinh ( x ) + C } \end{array}$$

一个函数 $f$ 的麦克劳林级数定义为：

$$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n$$

效果就是把它转成多项式。

$$\mathrm { e } ^ { x } = \sum _ { n = 0 } ^ { \infty } \frac { x ^ { n } } { n ! } = 1 + x + \frac { x ^ { 2 } } { 2 ! } + \frac { x ^ { 3 } } { 3 ! } + \cdots$$

$$\sin ( x ) = \sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } x ^ { 2 n + 1 } } { ( 2 n + 1 ) ! } = x - \frac { x ^ { 3 } } { 3 ! } + \frac { x ^ { 5 } } { 5 ! } - \frac { x ^ { 7 } } { 7 ! } + \cdots$$

$$\cos ( x ) = \sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } x ^ { 2 n } } { ( 2 n ) ! } = 1 - \frac { x ^ { 2 } } { 2 ! } + \frac { x ^ { 4 } } { 4 ! } - \frac { x ^ { 6 } } { 6 ! } + \cdots$$

$$\frac { 1 } { 1 - x } = \sum _ { n = 0 } ^ { \infty } x ^ { n } = 1 + x + x ^ { 2 } + x ^ { 3 } + \cdots$$

$$ { \ln ( 1 + x ) = \sum _ { n = 1 } ^ { \infty } - \frac { ( - 1 ) ^ { n } x ^ { n } } { n } = x - \frac { x ^ { 2 } } { 2 } + \frac { x ^ { 3 } } { 3 } - \frac { x ^ { 4 } } { 4 } + \cdots } $$

$$ { \ln ( 1 - x ) = \sum _ { n = 1 } ^ { \infty } - \frac { x ^ { n } } { n } = - x - \frac { x ^ { 2 } } { 2 } - \frac { x ^ { 3 } } { 3 } - \frac { x ^ { 4 } } { 4 } - \cdots } $$

$$\tan ^ { - 1 } ( x ) = x - \frac { x ^ { 3 } } { 3 } + \frac { x ^ { 5 } } { 5 } - \frac { x ^ { 7 } } { 7 } + \cdots = \sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } x ^ { 2 n + 1 } } { 2 n + 1 }$$

有什么用？

一个例子：

证明欧拉等式：

$$\mathrm { e } ^ { i \theta } = \cos ( \theta ) + i \sin ( \theta )$$

证明：

$$\begin{aligned} \mathrm { e } ^ { i \theta } & = 1 + ( i \theta ) + \frac { ( i \theta ) ^ { 2 } } { 2 ! } + \frac { ( i \theta ) ^ { 3 } } { 3 ! } + \frac { ( i \theta ) ^ { 4 } } { 4 ! } + \frac { ( i \theta ) ^ { 5 } } { 5 ! } + \frac { ( i \theta ) ^ { 6 } } { 6 ! } + \frac { ( i \theta ) ^ { 7 } } { 7 ! } + \cdots \\ & = 1 + i \theta - \frac { \theta ^ { 2 } } { 2 ! } - i \frac { \theta ^ { 4 } } { 3 ! } + \frac { \theta ^ { 4 } } { 4 ! } + i \frac { \theta ^ { 5 } } { 5 ! } - \frac { \theta ^ { 7 } } { 6 ! } - i \frac { \theta ^ { 7 } } { 7 ! } + \cdots \end{aligned}$$

我们把他们的实部和虚部分开，可以得到：

实部：

$$1 - \frac { \theta ^ { 2 } } { 2 ! } + \frac { \theta ^ { 4 } } { 4 ! } - \frac { \theta ^ { 6 } } { 6 ! } + \cdots = \cos ( \theta )$$

虚部：

$$\theta - \frac { \theta ^ { 3 } } { 3 ! } + \frac { \theta ^ { 5 } } { 5 ! } - \frac { \theta ^ { 7 } } { 7 ! } + \cdots = \sin ( \theta )$$

证完了。