MT【289】含参绝对值的最大值之三
已知$a>0$,函数$f(x)=e^x+3ax^2-2e x-a+1$,
(1)若$f(x)$在$[0,1]$上单调递减,求$a$的取值范围.
(2)$|f(x)|\le1$对任意$x\in[0,1]$恒成立,求$a$的取值范围.

解答:(1)略(2)的几何意义:
首先$|f(0)|\le1,|f(1)|\le1$得$1\le a\le \dfrac{e}{2}$
又$f^{''}(x)=e^x+6a>0$,故$f(x)$图像是下凸的.且$\int_0^1f(x)dx=[e^x+ax^3-ex^2+(1-a)x] {|^1}_0=0$
即$y=f(x)$图像在$x$ 轴下方的面积和上方的面积一样.
记$f^{'}(x_0)=e^x_0+6ax_0-2e=0$显然$x_0\in[0,1]$.如图,
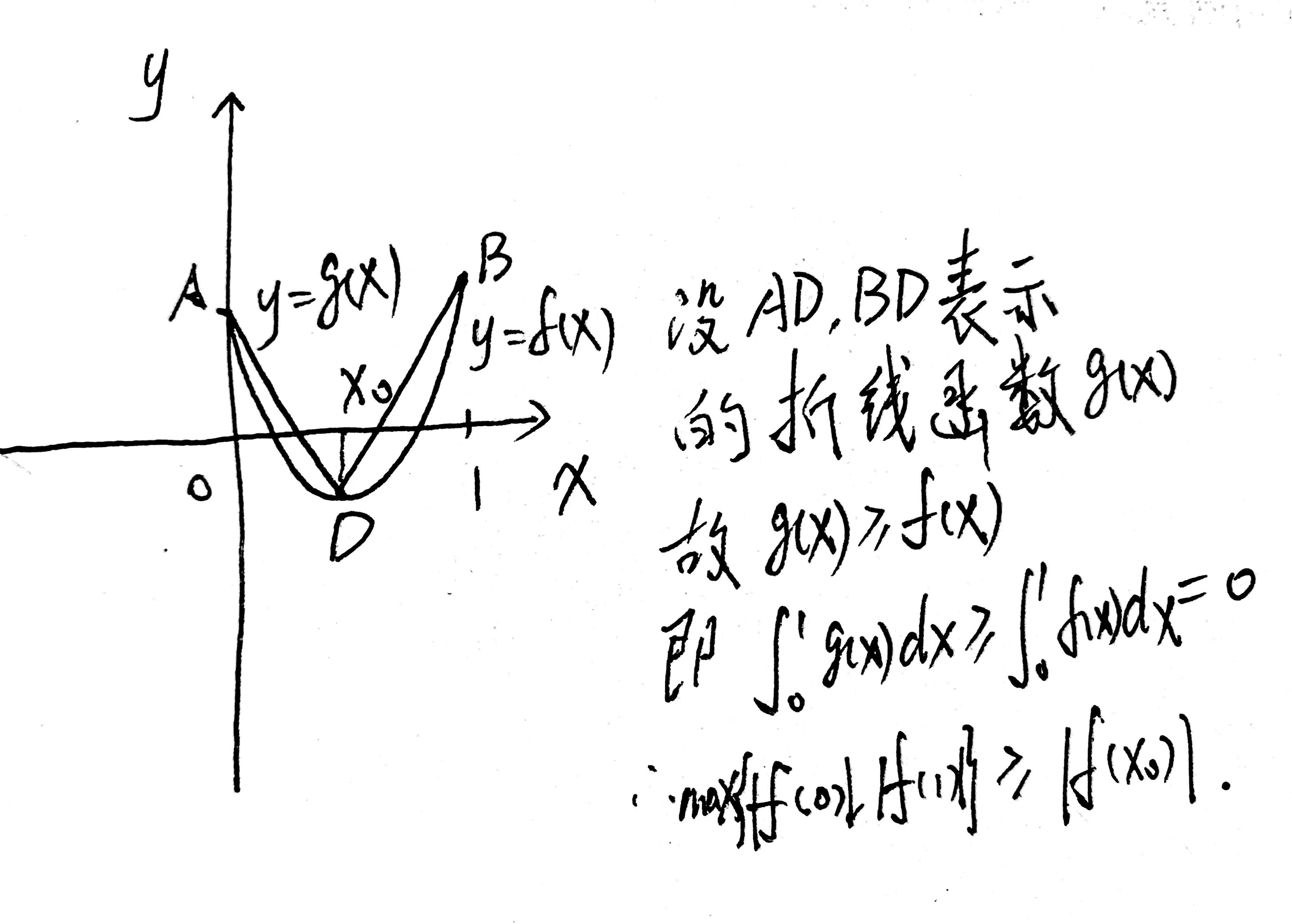
易知$|f(x)|_{max}=\max\{|f(0)|,|f(1)|\}$
所以$1\le a\le \dfrac{e}{2}$
附参考答案:

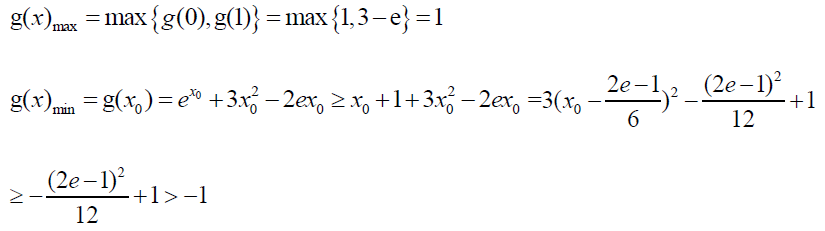
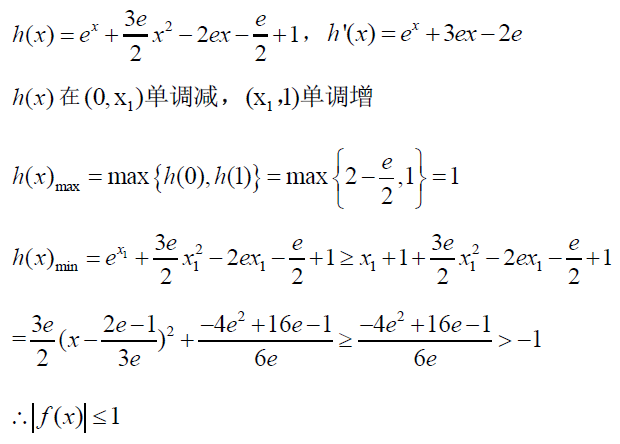
MT【289】含参绝对值的最大值之三的更多相关文章
- MT【270】含参绝对值函数最大之二
已知$f(x)=2ax\cos^2x+(a-1)\cos x-1,a>0$,记$|f(x)|$的最大值为$A$,1)求A.2)证明:$|-2a\sin 2x+(1-a)\sin x|\le 2A ...
- Java 解惑:Random 种子的作用、含参与不含参构造函数区别
Random 通常用来作为随机数生成器,它有两个构造方法: Random random = new Random(); Random random2 = new Random(50); 1.不含参构造 ...
- Java Random 含参与不含参构造函数的区别
##Random 通常用来作为随机数生成器,它有两个构造方法: Random random = new Random(); Random random2 = new Random(50); 1.不含参 ...
- Codeforces Round #320 (Div. 2) [Bayan Thanks-Round] E 三分+连续子序列的和的绝对值的最大值
E. Weakness and Poorness time limit per test 2 seconds memory limit per test 256 megabytes input sta ...
- MT【285】含参数函数绝对值的最大值
(浙江2013高考压轴题)已知$a\in R$,函数$f(x)=x^3-3x^2+3ax-3a+3$(2)当$x\in[0,2]$时,求$|f(x)|$的最大值. 分析:由题意$f^{'}(x)=3x ...
- MT【269】含参函数绝对值最大
设函数$f(x)=ax^2+(2b+1)x-a-2$($a,b\in\mathcal R$,$a\neq 0$). (1) 若$a=-2$,求函数$y=|f(x)|$在$[0,1]$上的最大值$M(b ...
- java abs(绝对值) , max(最大值),min(最小值) 方法的应用
在写程序是,我们常常会计算一个数的绝对值,这时我们可以使用java里的方法来计算 public class Demo1{ public static void main(String [] args) ...
- Python学习之高阶函数--嵌套函数、函数装饰器、含参函数装饰器
玩了一晚上王者,突然觉得该学习,然后大晚上的搞出来这道练习题,凌晨一点写博客(之所以这么晚就赶忙写是因为怕第二天看自己程序都忘了咋写的了),我太难了o(╥﹏╥)o 言归正传,练习题要求:构造类似京东的 ...
- 连续子数组的和的绝对值的最大值、最小值(非绝对值的话直接dp动态规划)
前缀和的思路: sum[i] = num[0]+num[1]+......+num[i-1] sum[j] = num[0]+num[1]+......+num[j-1] 那么:num[i]+num[ ...
随机推荐
- NYOJ-16-矩形嵌套 记忆化搜索
#include<iostream> #include<stdio.h> #include<string.h> #include<algorithm> ...
- c++入门之详细探讨类的一些行为
之前我们讨论过类成员的组成,尤其是成员函数,我们知道了定义一个类的时候,我们往往定义了:构造函数,析构函数,其他函数,以及友元函数(友元函数不是必须的). 同时,我们知道了这样一个事情:在定义一个对象 ...
- c++入门之输出文件流ofstream
# include "iostream" # include"fstream" int main() { using namespace std; ]; int ...
- NFV论文集(三)综述
一 文章名称:Dependability of the NFV Orchestrator: State of the Art and Research Challenges 发表时间:2018 期刊来 ...
- debian6保存iptables规则
iptables规则不保存,一旦机器重启规则就清空了,所以需要保存: iptables-save >/etc/iptables-script vi /etc/rc.local 然后在文件中输入: ...
- php使用gd库输出中文内容的图片
正如标题所说那样,本文只讨论输出内容全部为中文或者包含中文的情况.如果内容全是字母或者其他字符的话,可以参考这篇博客:生成验证码 问题 此处要注意,标题中为什么要区别windows和linux分别实现 ...
- How To: Capture Android & iOS Traffic with Fiddler
How To: Capture iOS Traffic with Fiddlerhttps://www.telerik.com/blogs/how-to-capture-ios-traffic-wit ...
- Linux下用rm删除的文件的恢复方法
Linux下用rm删除的文件的恢复方法_Linux教程_Linux公社-Linux系统门户网站https://www.linuxidc.com/Linux/2008-08/14744.htm linu ...
- 搞站思路 <陆续完善中>
只提供思路经验分享.不提供日站方法....一般站点那里最容易出现问题 入手思路: 主站一般都很安全.一般从二级域名下手 多看看那些大站新出来的测试分站点 猜路径别忘了google 考虑看站点下的rob ...
- jmeter环境配置
Java 8 安装 正常安装,一路默认就好,记住安装路径,配置环境变量时用得到.默认安装路径:C:\Program Files\Java\jdk1.8.0_91. 安装好之后会有两个文件夹一个是jdk ...
