2018 ACM-ICPC 中国大学生程序设计竞赛线上赛 H题 Rock Paper Scissors Lizard Spock.(FFT字符串匹配)

2018 ACM-ICPC 中国大学生程序设计竞赛线上赛：https://www.jisuanke.com/contest/1227

题目链接：https://nanti.jisuanke.com/t/26219

Rock Paper Scissors Lizard Spock

Description:

Didi is a curious baby. One day, she finds a curious game, which named Rock Paper Scissors Lizard Spock.

The game is an upgraded version of the game named Rock, Paper, Scissors. Each player chooses an option . And then those players show their choices that was previously hidden at the same time. If the winner defeats the others, she gets a point.

The rules are as follows.

Scissors cuts Paper

Paper covers Rock

Rock crushes Lizard

Lizard poisons Spock

Spock smashes Scissors

Scissors decapitates Lizard

Lizard eats Paper

Paper disproves Spock

Spock vaporizes Rock

(and as it always has) Rock crushes Scissors.

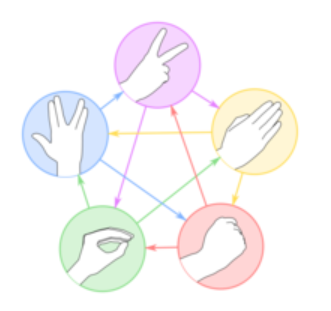
(this pic is from baike.baidu.com)

But
Didi is a little silly, she always loses the game. In order to keep her
calm, her friend Tangtang writes down the order on a list and show it
to her. Didi also writes down her order on another list, like

.

(Rock-R Paper-P Scissors-S Lizard-L Spock-K)

However, Didi may skip some her friends' choices to find the position to get the most winning points of the game, like

Can you help Didi find the max points she can get?

Input:

The first line contains the list of choices of Didi's friend, the second line contains the list of choices of Didi.

(1<=len(s2)<=len(s1)<=1e6)

Output:

One line contains an integer indicating the maximum number of wining point.

忽略每行输出的末尾多余空格

样例输入1

RRRRRRRRRLLL
RRRS

样例输出1

3

样例输入2

RSSPKKLLRKPS
RSRS

样例输出2

2
ACM-ICPC Asia Training League   宁夏理工学院

题解：

因为之前做过codeforces 528D. Fuzzy Search  ，感觉就不难了，你要是不会这题可以先去做cf528d，有个详细的题解：https://blog.csdn.net/u013368721/article/details/45565729

【FFT求字符串匹配的问题一般都是将模式串反转，然后将其与主串进行卷积运算】

枚举五种出拳方式，每种都做fft，最后扫一遍最大值即可求出最佳匹配出的赢的最大次数。（具体fft原理不懂orz，我就是套着原来板子写的...）

#include<bits/stdc++.h>
#define CLR(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long ll;
const int N = <<;
const double PI = acos(-1.0);
int n, m;
struct Complex {
    double x,y;
    Complex(double _x = 0.0,double _y = 0.0){
        x = _x; y = _y;
    }
    Complex operator -(const Complex &b)const{
        return Complex(x-b.x,y-b.y);
    }
    Complex operator +(const Complex &b)const{
        return Complex(x+b.x,y+b.y);
    }
    Complex operator *(const Complex &b)const{
        return Complex(x*b.x-y*b.y,x*b.y+y*b.x);
    }
    Complex operator * (const double &b)const{
        return Complex(x * b,y * b);
    }
    Complex operator / (const double &b)const{
        return Complex(x / b,y / b);
    }
};
void change(Complex y[], int len) {
    int i, j, k;
    for(i = , j = len/;i <len-;i++) {
        if(i < j)swap(y[i],y[j]);
        k = len/;
        while(j >= k) {
            j -= k;
            k /= ;
        }
        if(j < k) j += k;
    }
}
void fft(Complex y[],int len,int on) {
    change(y,len);
    for(int h = ; h <= len; h <<= ) {
        Complex wn(cos(-on**PI/h),sin(-on**PI/h));
        for(int j = ;j < len;j+=h) {
            Complex w(,);
            for(int k = j;k < j+h/;k++) {
                Complex u = y[k];
                Complex t = w*y[k+h/];
                y[k] = u+t;
                y[k+h/] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -)
        for(int i = ;i < len;i++)
            y[i].x /= len;
}
Complex a[N], b[N], c[N];
char s[N], t[N];
int sum[N];
int main() {
    int i, j, ans = , ma, nn;
    scanf("%s %s", s, t);
    n = strlen(s);
    m = strlen(t);
    reverse(t, t+m);
    ma = max(n, m);  nn = ;
    while(nn <  * ma) nn<<=;
    CLR(c, ); CLR(sum, );
    //R vs L S
    CLR(a, ); CLR(b, );
    for(i = ; i < n; ++i) a[i].x = (s[i]=='L'||s[i]=='S');
    for(i = ; i < m; ++i) b[i].x = (t[i]=='R');
    fft(a, nn, ); fft(b, nn, );
    for(i = ; i < nn ;++i) c[i] = a[i] * b[i];
    fft(c, nn, -);
    for(i = m-; i < n; ++i)
        sum[i] += (int)(c[i].x+0.5);
    //P vs R K
    CLR(a, ); CLR(b, );
    for(i = ; i < n; ++i) a[i].x = (s[i]=='R'||s[i]=='K');
    for(i = ; i < m; ++i) b[i].x = (t[i]=='P');
    fft(a, nn, ); fft(b, nn, );
    for(i = ; i < nn ;++i) c[i] = a[i] * b[i];
    fft(c, nn, -);
    for(i = m-; i < n; ++i)
        sum[i] += (int)(c[i].x+0.5);
    //S vs P L
    CLR(a, ); CLR(b, );
    for(i = ; i < n; ++i) a[i].x = (s[i]=='P'||s[i]=='L');
    for(i = ; i < m; ++i) b[i].x = (t[i]=='S');
    fft(a, nn, ); fft(b, nn, );
    for(i = ; i < nn ;++i) c[i] = a[i] * b[i];
    fft(c, nn, -);
    for(i = m-; i < n; ++i)
        sum[i] += (int)(c[i].x+0.5);
    //L vs P K
    CLR(a, ); CLR(b, );
    for(i = ; i < n; ++i) a[i].x = (s[i]=='P'||s[i]=='K');
    for(i = ; i < m; ++i) b[i].x = (t[i]=='L');
    fft(a, nn, ); fft(b, nn, );
    for(i = ; i < nn ;++i) c[i] = a[i] * b[i];
    fft(c, nn, -);
    for(i = m-; i < n; ++i)
        sum[i] += (int)(c[i].x+0.5);
    //K vs R S
    CLR(a, ); CLR(b, );
    for(i = ; i < n; ++i) a[i].x = (s[i]=='R'||s[i]=='S');
    for(i = ; i < m; ++i) b[i].x = (t[i]=='K');
    fft(a, nn, ); fft(b, nn, );
    for(i = ; i < nn ;++i) c[i] = a[i] * b[i];
    fft(c, nn, -);
    for(i = m-; i < n; ++i)
        sum[i] += (int)(c[i].x+0.5);
    for(i = m-; i < n; ++i) ans = max(ans, sum[i]);
    printf("%d\n", ans);
    return ;
}