用 TensorFlow 实现 k-means 聚类代码解析

k-means 是聚类中比较简单的一种。用这个例子说一下感受一下 TensorFlow 的强大功能和语法。

一、 TensorFlow 的安装

按照官网上的步骤一步一步来即可，我使用的是 virtualenv 这种方式。

二、代码功能

在$[0,0]$ 到 $[1,1]$ 的单位正方形中，随机生成 $N$ 个点，然后把这 $N$ 个点聚为 $K$ 类。
最终结果如下，在 0.29s 内，经过 17 次迭代，找到了4个类的中心，并给出了各个点归属的类。

Found in 0.29 seconds

iterations, 17

Centroids:  [[ 0.24536976  0.73962539]

 [ 0.25338876  0.23666154]

 [ 0.75791192  0.25526255]

 [ 0.7544601   0.75478882]]

Cluster assignments: [1 1 2 ..., 0 2 1]

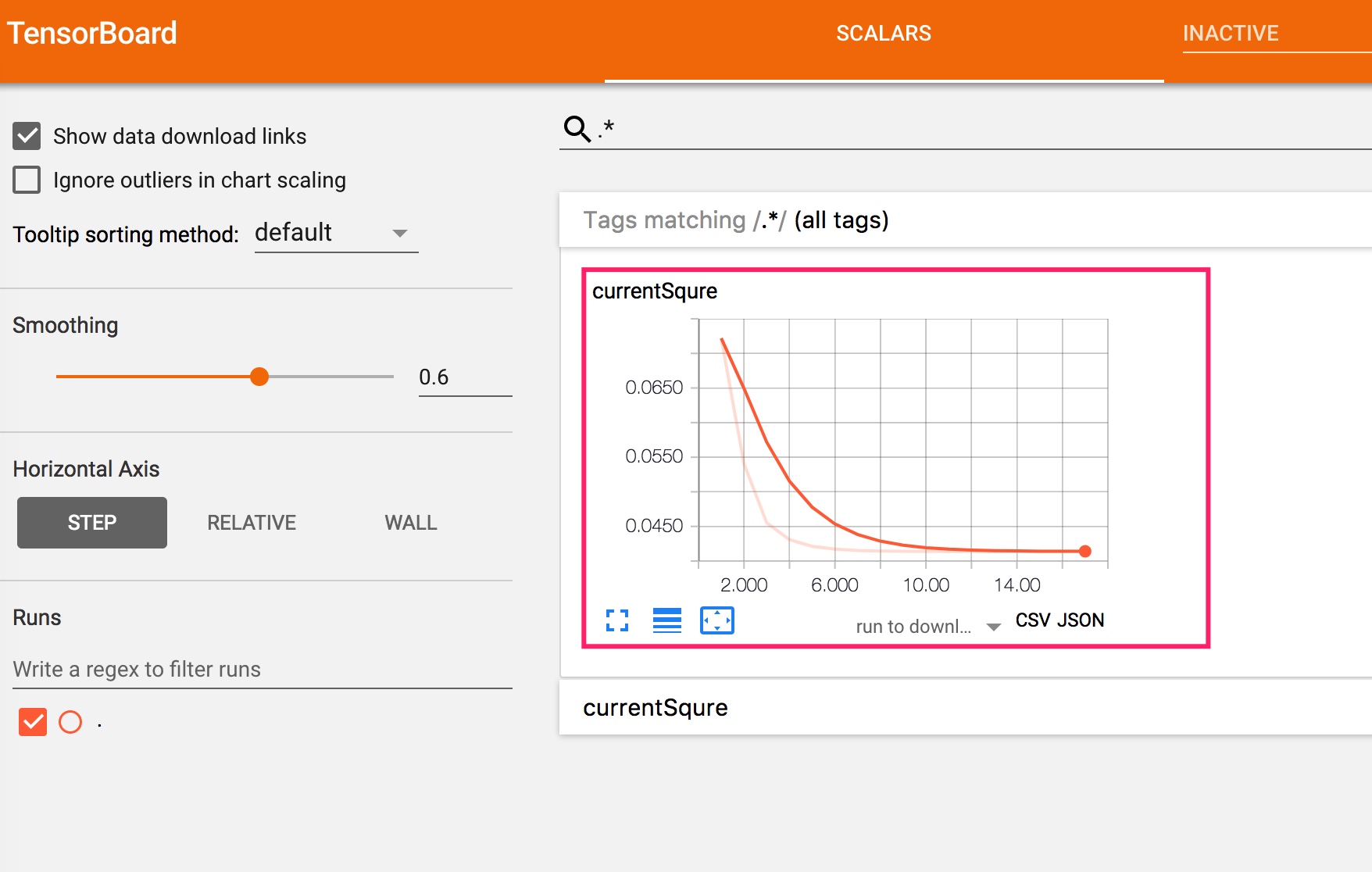
而最小平方误差的变化如下。可以看出逐渐变小。

三、代码解析

引入相应的库

# copy from https://gist.github.com/dave-andersen/265e68a5e879b5540ebc

# add summary

import tensorflow as tf

import numpy as np

import time

定义问题规模以及一些变量

N=10000  # 要被聚类的点的数目

K=4      # 被聚为K类

MAX_ITERS = 1000 #最大迭代数目

test_writer = tf.summary.FileWriter("log")  # TensorBorad 数据存储数目

start = time.time() # 起始时间

初始化

points = tf.Variable(tf.random_uniform([N,2])) #随机生成N个点

cluster_assignments = tf.Variable(tf.zeros([N], dtype=tf.int64)) #这个变量表示每个点所属的类别，初始化为第0类

# Silly initialization:  Use the first K points as the starting

# centroids.  In the real world, do this better.

centroids = tf.Variable(tf.slice(points.initialized_value(), [0,0], [K,2])) # 每个类的中心

下面用数学表达式来说明一下，这里下标不是从 0 开始。
$N$ 个点 points 用下面式子来表达。
\[[[x_1,y_1],[x_2,y_2],...[x_n,y_n]]\]
每个点所属类别 cluster_assignments 用下面式子表达：
\[[\lambda_1,\lambda_2,...\lambda_n]\]
其中，$\lambda_i<k$
每个类的中心 centroids 用下面是式子表达：
\[[[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky]]\]

计算每个点距离每个类中心的距离
```
# Replicate to N copies of each centroid and K copies of each

# point, then subtract and compute the sum of squared distances.

rep_centroids = tf.reshape(tf.tile(centroids, [N, 1]), [N, K, 2])

rep_points = tf.reshape(tf.tile(points, [1, K]), [N, K, 2])

sum_squares = tf.reduce_sum(tf.square(rep_points - rep_centroids),

                            reduction_indices=2)
```
先看tf.tile 函数。根据文档，tf.tile(centroids, [N, 1])函数执行完，结果如下：
\[[[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky],[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky],...[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky]]\]
即有 $NK$个点。然后经过 tf.reshape 函数，结果如下：
\[[[[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky]],\\
[[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky]],\\
...\\
[[c_1x,c_1y],[c_2x,c_2y],...[c_kx,c_ky]]]\]
即可以看做一个$N \times K$的矩阵，每一个元素是一个点。这就是 rep_centroids的大致理解。
同理可得，rep_points结果如下：
\[[[[x_1,y_1],[x_1,y_1],...[x_1,y_1]],\\
[[x_2,y_2],[x_2,y_2],...[x_2,y_2]],\\
...\\
[[x_n,y_n],[x_n,y_n],...[x_n,y_n]]]\]
也可以看做一个$N \times K$的矩阵。每一行所有元素都相同，是第$i$个点。
tf.square(rep_points - rep_centroids)结果如下：
\[[[[[(x_1-c_1x)^2,(y_1-c_1y)^2],[(x_1-c_2x)^2,(y_1-c_2y)^2],...[(x_1-c_kx)^2,(y_1-c_ky)^2]],\\
[[(x_2-c_1x)^2,(y_2-c_1y)^2],[(x_2-c_2x)^2,(y_2-c_2y)^2],...[(x_2-c_kx)^2,(y_2-c_ky)^2]],\\
...\\
[[(x_n-c_1x)^2,(y_n-c_1y)^2],[(x_n-c_2x)^2,(y_n-c_2y)^2],...[(x_n-c_kx)^2,(y_n-c_ky)^2]]]\]
而sum_squares的结果，是把$N \times K$矩阵的每一个元素变为一个值，如下：
\[[[[d_{11},d_{12},...d_{1k}],\\
[d_{11},d_{22},...d_{2k}],\\
...\\
[d_{n1},d_{n2},...d_{nk}]]\]
其中
\[d_{ij} = (x_i-c_jx)^2+(y_i-c_jy)^2 \]
即 $d_{ij}$ 是第 $i$ 个点和第 $k$ 个类的中心的距离。

判断点所属的类

# Use argmin to select the lowest-distance point

best_centroids = tf.argmin(sum_squares, 1)

did_assignments_change = tf.reduce_any(tf.not_equal(best_centroids,

                                                    cluster_assignments))

best_centroids是一行中，最小的数值的下标，即某个点应该被判定为哪一类。
did_assignments_change表示新判定的类别和上次迭代的类别有没有变化。

更新类别的中心
```
def bucket_mean(data, bucket_ids, num_buckets):

total = tf.unsorted_segment_sum(data, bucket_ids, num_buckets)

count = tf.unsorted_segment_sum(tf.ones_like(data), bucket_ids, num_buckets)

return total / count

# 新的分簇点

means = bucket_mean(points, best_centroids, K)

currentSqure = tf.reduce_sum(tf.reduce_min(sum_squares,1))/N

tf.summary.scalar('currentSqure', currentSqure)

merged = tf.summary.merge_all()
```
先看bucket_mean 函数。data 被传入了被聚类的$N$个点，bucket_ids被传入了每个点所属的类别，num_buckets 是类别的数目。
tf.unsorted_segment_sum可以理解为根据第二个参数(bucket_ids)，把data分为不同的集合，然后分别对每一个集合求和。

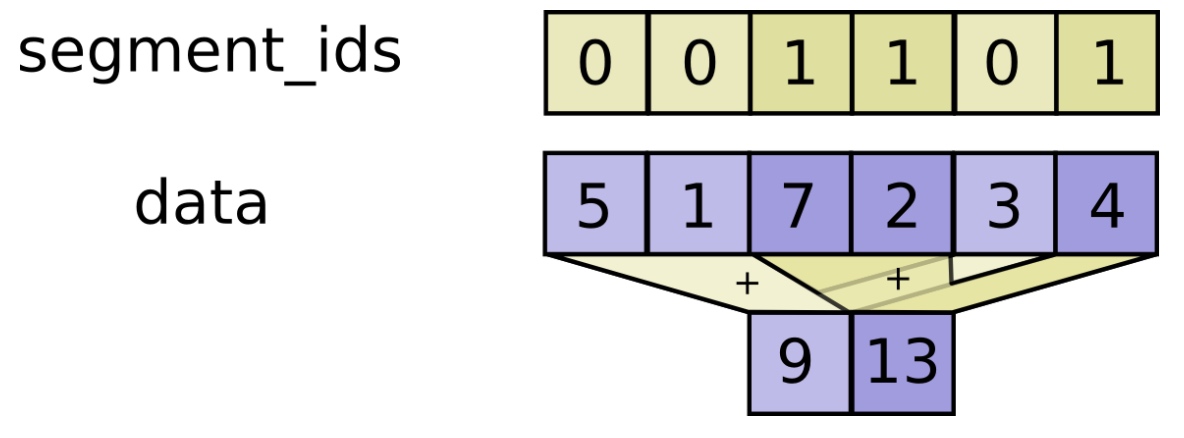
因此total即把$N$个点分为$K$个集合，然后对每一个集合求和。count则是求出每一个集合的个数。相除即得到每一个集合（即每一个类）的中心。
means即新划分的各个类的中心。
currentSqure是当前划分的最小平方误差。然后把变量计入日志中。

指定迭代结构

# Do not write to the assigned clusters variable until after

# computing whether the assignments have changed - hence with_dependencies

with tf.control_dependencies([did_assignments_change]):

    do_updates = tf.group(

        centroids.assign(means),

        cluster_assignments.assign(best_centroids))

如果did_assignments_change有变化，那么把means赋值给centroids，把best_centroids赋值给cluster_assignments。

启动 session

init = tf.initialize_all_variables()

sess = tf.Session()

sess.run(init)

changed = True

iters = 0

进行迭代

while changed and iters < MAX_ITERS:

    iters += 1

    [summary,changed, _] = sess.run([merged,did_assignments_change, do_updates])

    test_writer.add_summary(summary,iters) #写入日志

test_writer.close()

[centers, assignments] = sess.run([centroids, cluster_assignments])

end = time.time()

print ("Found in %.2f seconds" %(end-start))

print(  "iterations,",iters )

print("Centroids: " ,centers)

print( "Cluster assignments:",assignments)

print("cluster_assignments",cluster_assignments)

指定最多迭代次数。值得注意的是，每一次迭代，都要把数据显式写入log中。

四、感受

机器学习的计算量太大了，并行性也很明显。
对结果要有评估，否则意义不大。
这个例子中，随机生成的数据，根据算也可以进行聚类。但是意义显然不大。
有一个图形化的界面很重要。TensorBoard 可以直观看出平方误差在不断变化

五、参考