关于manacher

由一个题引入：

求一个串A的最长回文串:
　　A=abababa
最长回文串长度：5（ababa）

先思考用hash怎么做？

一、暴力
　　枚举左端，右端点（确定一个区间），线性扫一遍当前区间。
　　Ans=max(ans);

　　时间复杂度：O(n^3)
　　貌似也有O（n^2）的暴力，在此不再赘述。
二、哈希
　　分设两个hash数组， ha1记录前缀， ha2记录后缀。
　　对于任意[l,r] 若ha1[l,mid]==ha2[mid+1,r],则为回文串
　　Ans=max(ans);

　　时间复杂度：O(nlog 2 n)
三、manacher
　　而manacher算法也可以在O(n)的时间内求出答案

定义数组 p[i]表示以i为中心的(包含i个这个字符)回文串半长。

将字符串s从前扫到后，来计算p[i]，则最大的p[i]就是最长回文串长度。

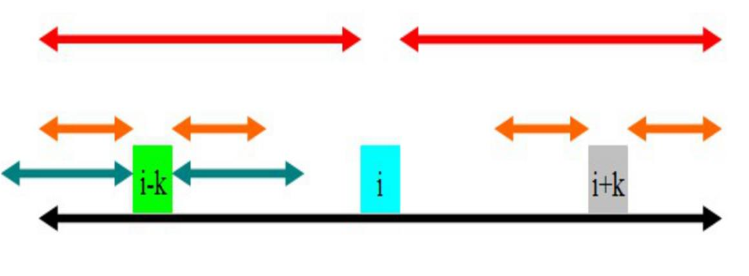
算法流程：
由于s是从前扫描到最后的,所以需要计算p[i]时一定计算好了p[1]~~p[i-1]
假设现在扫描到了i+k这个位置,现在需要计算p[i+k]
定义maxlen是位置i+k位置前所有回文串中能延伸到的最有右端的位置,即maxlen=p[i]+i;
p[i]表示半径长,i 表示目前最长的位置。

有两种情况：

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define m(s) memset(s,0,sizeof s);
using namespace std;
const int N=1e6+;
int l,cas,len,p[N<<];
char s[N],S[N<<];
void manacher(){
    int ans=,id=,mx=-;
    for(int i=;i<l;i++){
        if(id+mx>i) p[i]=min(p[id*-i],id+mx-i);
        while(i-p[i]->=&&i+p[i]+<=l&&S[i-p[i]-]==S[i+p[i]+]) p[i]++;
        if(id+mx<i+p[i]) id=i,mx=p[i];
        ans=max(ans,p[i]);
    }
    printf("Case %d: %d\n",++cas,ans);
}
int main(){
    while(scanf("%s",s)==){
        if(s[]=='E') break;
        len=strlen(s);m(p);m(S);
        l=-;
        for(int i=;i<len;i++) S[++l]='#',S[++l]=s[i];
        S[++l]='#';
        manacher();
    }
    return ;
}

关于manacher的应用：

应用1.输入一个字符串Str，输出Str里最长回文子串的长度。 模板的用法

应用2.判断是否能将字符串S分成三段非空回文串。

【输入说明】
第一行一个整数T，表示数据组数。
对于每一个组，仅包含一个由小写字母组成的串。
【输出说明】
对于每一组，单行输出"Yes" 或 "No“

解：

 对原串前缀和后缀作一个01标记pre[i],suf[i]表示1-i和i-n能否能形成回文。记以i为中心的回文半径为r(i)。
 这些都可以在O(N)时间内求出。也可以使用Hash+二分等方法O(NlogN)内求出。
 我们考虑中间一个回文串的位置，不妨设它是奇数长度（偶数类似）。
 那么问题变成了求一个i和d使得1<=d<=r(i)且pre[i-d]和suf[i+d]为真。
 枚举i，实际上就是问pre[i-r(i)..i-1]和suf[i+1..i+r(i)]取反后这两段有没有一个位置两者均为1，也就是and后不为0，暴力压位即可。
推荐：HDU 5340

一世安宁