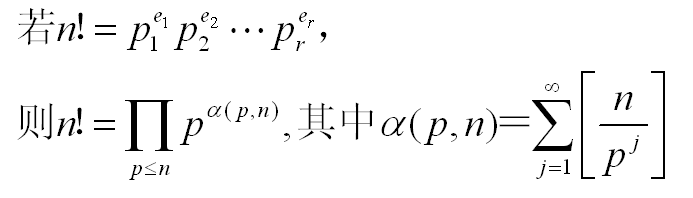南阳nyoj 509 因子和阶乘
因子和阶乘
- 描述
- 给你一个正整数n,把n!=1x2x3x.....xn分解成素因子相乘的形式,并从小到大输出每个素因子的指数,但要保证最后输出的素因子个数不为0。例如825应表示为0,1,2,0,1表示分别有0,1,2,0,1个2,3,5,7,11。
- 输入
- 第一行有一个整数n(0<n<10000),表示有n组测试数据;
接下来n行每行有一个整数 m(1<m<10000) - 输出
- 从小到大输出m分解成素因子相乘后各个素因子对应的指数
- 样例输入
-
2
5
53 - 样例输出
-
3 1 1
49 23 12 8 4 4 3 2 2 1 1 1 1 1 1 1 做这一题是,不知道如何处理这个N!,如果可以转化成整数,那可以用以前的知识解决了。但是
N很大的时候,就不行了。
理论依据:
也可以写成
num=[N/pi^1]+ [N/pi^2]+ …… + [N/pi^n] 其中[]为取整
求N!有几个要注意的地方。
1.最大的质因子不会超过N,
2.关于公式的转化:
式子中把一些东西看成一个整体。举例:
num=N/pi^1+N/pi^2+N/pi^3;
==>
N/p1^1+(N/p1^1)/p1^1+((N/p1^1)/p1^1)/p1^1;
这样的话就可以写成一个solve函数。#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std; bool s[];
int prime[],len;
int Flag; void make_prime()//素数获取
{
int i,j;
len=;
for(i=;i<=;i++)
if(s[i]==false)
{
prime[++len]=i;
for(j=i*;j<=;j=j+i)
s[j]=true;
}
} void solve(int n,int m)//num=[N/pi^1]+ [N/pi^2]+ …… + [N/pi^n]
{
int i,k=;
while(n)
{
n=n/m;
k=k+n;
}
if(Flag==)
{
printf("%d",k);
Flag=;
}
else printf(" %d",k);
} int main()
{
int T,n,i;
make_prime();
while(scanf("%d",&T)>)
{
while(T--)
{
scanf("%d",&n);
Flag=;
for(i=;prime[i]<=n;i++)
solve(n,prime[i]);
printf("\n");
}
}
return ;
}
南阳nyoj 509 因子和阶乘的更多相关文章
- ny509 因子和阶乘
因子和阶乘 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描述 给你一个正整数n,把n!=1x2x3x.....xn分解成素因子相乘的形式,并从小到大输出每个素因子的指数 ...
- 南阳nyoj 56 阶乘因式分解(一)
阶乘因式分解(一) 时间限制:3000 ms | 内存限制:65535 KB 难度:2 描述 给定两个数m,n,其中m是一个素数. 将n(0<=n<=10000)的阶乘分解质因数, ...
- nyoj 65-另一种阶乘问题 (Java 高精度)
65-另一种阶乘问题 内存限制:64MB 时间限制:3000ms 特判: No 通过数:16 提交数:18 难度:1 题目描述: 大家都知道阶乘这个概念,举个简单的例子:5!=1*2*3*4*5.现在 ...
- NYOJ题目28大数阶乘
-------------------------------------祭出BigInteger AC代码: import java.math.BigInteger; import java.uti ...
- words2
餐具:coffee pot 咖啡壶coffee cup 咖啡杯paper towel 纸巾napkin 餐巾table cloth 桌布tea -pot 茶壶tea set 茶具tea tray 茶盘 ...
- 算法入门笔记------------Day4
1.WERTYU 输入一个错位后敲出的字符串,输出打字员本来想打出的字 #include<stdio.h> char *s="`1234567890-=QWERTYUIOP[]\ ...
- Zerojudge解题经验交流
题号:a001: 哈囉 背景知识:输出语句,while not eof 题号:a002: 簡易加法 背景知识:输出语句,while not eof,加法运算 题号:a003: 兩光法師占卜術 背景知识 ...
- bzoj千题计划267:bzoj3129: [Sdoi2013]方程
http://www.lydsy.com/JudgeOnline/problem.php?id=3129 如果没有Ai的限制,就是隔板法,C(m-1,n-1) >=Ai 的限制:m减去Ai &l ...
- 同余&逆元简单总结
# 同余&逆元 1. 同余 1. 同余的基本概念及性质 若\(x\)%\(m=a\)即m是 x-a 的一个因子, 则称x与a关于m同余,记作:\[x \equiv a(mod \;m)\] 同 ...
随机推荐
- Day 31 面向对象考试题 第四次考试.
一 基础知识和函数: 1.文件操作有哪些模式?请简述各模式的作用 r ,只读模式[默认模式,文件必须存在,不存在则抛出异常] w,只写模式[不可读:不存在则创建:存在则清空内容] x, 只写模式[不可 ...
- Console命令,让js调试更简单
一.显示信息的命令 console.log("normal"); // 用于输出普通信息 console.info("information"); // 用于输 ...
- 926. Flip String to Monotone Increasing
A string of '0's and '1's is monotone increasing if it consists of some number of '0's (possibly 0), ...
- BZOJ 1008--[HNOI2008]越狱(容斥&快速幂)
1008: [HNOI2008]越狱 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 12593 Solved: 5439[Submit][Status ...
- tomcat安装配置常见问题详解
历经波折,终于把tomcat装好了.记录下过程供自己和后来的初学者参考吧! 本文先后介绍了tomcat的下载安装方法.安装和启动不成功的常见原因 以及启动tomcat后如何配置上下文. 一.下载安装 ...
- jvm(2)类的初始化(二)和实例化
深入理解Java对象的创建过程:类的初始化与实例化 对象实例化内存分析: 对内存分配情况分析最常见的示例便是对象实例化: Object obj = new Object(); 这段代码的执行会涉及ja ...
- 逆向工程生成的Mapper.xml以及*Example.java详解
逆向工程生成的接口中的方法详解 在我上一篇的博客中讲解了如何使用Mybayis逆向工程针对单表自动生成mapper.java.mapper.xml.实体类,今天我们先针对mapper.java接口中的 ...
- Xcode 9 Analyzing Crash Reports
Analyzing Crash Reports After you distribute your app for testing by using TestFlight or after you m ...
- POJ 1146
#include <iostream> #include <algorithm> #define MAXN 55 using namespace std; char _m[MA ...
- QuantLib 金融计算——修复 BatesProcess 中的两个 Bug
QuantLib 金融计算--修复 BatesProcess 中的两个 Bug 我发现了 BatesProcess 中的两个 Bug: 基类 HestonProcess::factors 的返回值取决 ...