【四校联考】【比赛题解】FJ NOIP 四校联考 2017 Round 7

此次比赛为厦门一中出题。都是聚劳，不敢恭维。

莫名爆了个0，究其原因，竟然是快读炸了……很狗，很难受。

话不多说，来看看题：

【T1】

题意：

样例：

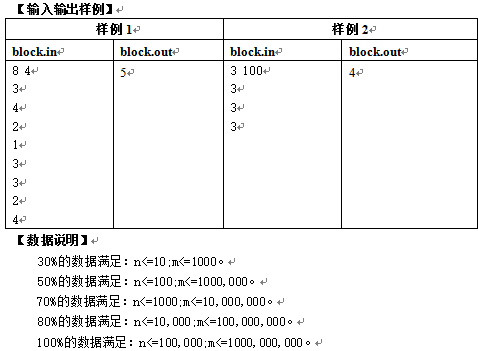
PS：1<=h[i]<=100000。

题解：

假设\(max\left(h_{i}\right)=M\)，可以发现最大高度不超过\(M+n\)。

而用\(m\)块砖，向上最多能搭\(\sqrt{m}\)个。

故最大高度为\(M+min\left(n,\sqrt{m}\right)\)。

而最低高度为\(M\)（或\(M+1\)）。

也就是说，高度的范围不超过3163。

而可以看出对于高度\(h\)，能否搭建起高\(h\)的塔是单调的。

如果我们二分高度\(h\)，计算能否搭建，就能够较快出解。

考虑在第\(i\)列搭上\(h\)的高度，那么最少需要多少砖块呢？

当然是按照金字塔形斜向下，直到遇到第一个可以作为支撑的砖块。

设\(left\left[i\right]\left[h\right]\)为坐标\(\left(i,h\right)\)向左斜向下遇到的第一个砖块的标号，\(right\left[i\right]\left[h\right]\)则为向右斜向下，若不存在，则值为0。

那么最少需要的砖块数（包括已经搭建的）等于：

\(Sum[i][h]=h(right[i][h]-left[i][h]-1)-\frac{(i-left[i][h])(i-left[i][h]-1)}{2}-\frac{(right[i][h]-i)(right[i][h]-i-1)}{2}\)。

而需要多搭的为：\(Sum[i][h]-(sum_{right[i][h]-1}-sum_{left[i][h]})\)，其中\(sum\)为前缀和。

现在，如何快速算出\(left\)和\(right\)呢？

看往左斜向下的，容易发现，\(k\)能够阻挡\((i,h)\)当且仅当\(h_{k}-k\geqslant h-i\)。

而对于向右下方的，我们有，\(k\)能够阻挡\((i,h)\)当且仅当\(h_{k}+k\geqslant h+i\)。

考虑记录下\(L_{k}=h_{k}-k\)与\(R_{k}=h_{k}+k\)。

那么我们就是对特定\(i,h\)要求出从右往左第一个\(k\)使得\(L_{k}\geqslant h-i\)，求出从左往右第一个\(k\)使得\(R_{k}\geqslant h+i\)。

这是单调栈的模型，先把\(L_{k}\)和\(R_{k}\)用单调栈维护一遍。

而在计算过程中，\(h+i\)与\(h-i\)是单调递增或递减的，这有了双指针扫描的可能性。

这就是整体思路，代码有点复杂……

 #include<cstdio>
 #define F(i,a,b) for(int i=a;i<=b;++i)
 #define dF(i,a,b) for(int i=a;i>=b;--i)
 int n,m,h[],Ans,M;
 long long sum[];
 int left[][],lp,right[][],rp;
 int L[],R[];
 inline int Max(int x,int y){return x>y?x:y;}
 void init(){
     scanf("%d%d",&n,&m);
     F(i,,n) scanf("%d",h+i), M=Max(M,h[i]);
     F(i,,n) sum[i]=sum[i-]+h[i];
     lp=;
     F(i,,n){
         while(lp&&left[lp][]<=h[i]-i) --lp;
         left[++lp][]=h[i]-i;
         left[lp][]=i;
     } left[][]=;
     rp=;
     dF(i,n,){
         while(rp&&right[rp][]<=h[i]+i) --rp;
         right[++rp][]=h[i]+i;
         right[rp][]=i;
     } right[][]=;
 //    F(i,1,lp) printf("(%d,%d) ",left[i][0],left[i][1]); puts("");
 //    F(i,1,rp) printf("(%d,%d) ",right[i][0],right[i][1]); puts("");
     Ans=M;
 }
 int main(){
     freopen("block.in","r",stdin);
     freopen("block.out","w",stdout);
     init();
     int l=M+, r=M+, mid, ok;
     while(l<=r){
         mid=(l+r)>>;
         ok=;
 //        printf("%d:\n",mid);
         for(int i=,pos=;i<=n;++i){
             L[i]=;
             if(pos!=lp&&left[pos+][]>=mid-i) ++pos;
             if(left[pos][]>=mid-i) L[i]=left[pos][]+;
         }
 //        for(int i=1;i<=n;++i) printf("%d ",L[i]); puts("");
         for(int i=n,pos=;i>=;--i){
             R[i]=;
             if(pos&&right[pos+][]>=mid+i) ++pos;
             if(right[pos][]>=mid+i) R[i]=right[pos][]-;
         }
 //        for(int i=1;i<=n;++i) printf("%d ",R[i]); puts("");
         F(i,,n){
             if(L[i]==||R[i]==) continue;
             long long Sum=
             (long long)mid*(R[i]-L[i]+)-
             (long long)(i-L[i]+)*(i-L[i])/-
             (long long)(R[i]-i+)*(R[i]-i)/-
             (sum[R[i]]-sum[L[i]-]);
 //            printf("%d:%lld ",i,Sum);
             if(Sum<=m) {ok=; break;}
         }//puts("");
         if(ok) l=mid+, Ans=mid;
         else r=mid-;
     }
     printf("%d",Ans);
     return ;
 }

【T2】

题意：

样例：

题解：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cassert>
 using namespace std;
 #define rep(i,a,n) for (int i=a;i<n;i++)
 #define per(i,a,n) for (int i=n-1;i>=a;i--)
 typedef long long ll;
 // head

 const int N=;
 int n,m,cnt0[N],cnt1[N];
 ll m0,md,cnt2[N];
 int main() {
     freopen("cake.in","r",stdin);
     freopen("cake.out","w",stdout);
     scanf("%d%d",&m,&n);
     scanf("%lld%lld",&m0,&md);
     rep(i,,m+) {
 //        printf("%lld\n",m0);
         cnt0[m0]++;
         m0=(m0*+md)%(n+);
     }
 //    puts("");
     scanf("%lld%lld",&m0,&md);
     rep(i,,n+) {
 //        printf("%lld\n",m0);
         cnt1[m0]++; cnt2[m0]+=m0;
         m0=(m0*+md)%(m+);
     }
     int x=; ll sx=;
     rep(i,,m+) cnt1[i]+=cnt1[i-],cnt2[i]+=cnt2[i-];
     ll ans=cnt2[m];
 //    puts("");
     rep(i,,n+) {
         rep(j,,cnt0[i]) {
             x++; sx+=i;
             int y=cnt1[m-x];
             assert(x<=m&&y<=n);
             ll ret=(ll)(m-x)*(n-y)+cnt2[m-x]+sx;
 //            printf("%lld\n",ret);
             ans=min(ans,ret);
         }
     }
     printf("%lld\n",ans);
 }

【T3】

题意：

题解：

我个人不会做……有待学习。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #define rep(i,a,b) for(int i=(a);i<=(b);i++)
 #define per(i,a,b) for(int i=(a);i>=(b);i--)
 #define Rep(i,x) for(int i=head[x];i+1;i=nxt[i])
 #define pb push_back
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int N=4e6+;
 const int M=8e6+;
 inline void read(int &x){x=;char ch=getchar(); while(ch<'') ch=getchar(); while(ch>=''){x=x*+ch-;ch=getchar();}}
 inline void judge()
 {
     freopen("tree.in","r",stdin);
     freopen("tree.out","w",stdout);
 }
 int fa[N],head[N],nxt[M],to[M],e,w[M],id[M];
 int wod[N];
 int son[N][],pd[N],tp[N];
 inline void init(){memset(head,-,sizeof(head)); e=;}
 inline void add_edge(int x,int y,int z,int ii){to[e]=y;w[e]=z;nxt[e]=head[x];id[e]=ii;head[x]=e++;}
 ll ma[N][],ans[N][];
 inline void Insert(int x,ll y,int cjl,int ii)
 {
     if(ma[x][]<y){ma[x][]=ma[x][];ma[x][]=y;son[x][]=son[x][];son[x][]=cjl;pd[x]=ii;}
     else if(y>ma[x][]){ma[x][]=y;son[x][]=cjl;}
 }
 void dfs(int x)
 {
     ma[x][]=ma[x][]=;Rep(i,x)
     {
         int j=to[i]; if(j==fa[x]) continue; fa[j]=x; tp[j]=id[i];
         dfs(j); Insert(x,ma[j][]+(ll)w[i],j,tp[j]);
     }
 }
 inline void Insert3(int x,ll y)
 {
     if(ma[x][]<y){ma[x][]=ma[x][];ma[x][]=y;}
     else if(y>ma[x][])ma[x][]=y;
 }
 void dfs3(int x,int f,int pp)
 {
     ma[x][]=ma[x][]=;ans[pp][]=;Rep(i,x)
     {
         int j=to[i]; if(j==f) continue;
         dfs3(j,x,id[i]); Insert3(x,ma[j][]+(ll)w[i]);
         ans[pp][]=max(ans[pp][],ans[id[i]][]);
     }ans[pp][]=max(ans[pp][],ma[x][]+ma[x][]);
 }
 vector<int> tt,Route,Rid,tt2;
 void dfs2(int x)
 {
     tt.push_back(x); if(pd[x])tt2.push_back(pd[x]);
     if(son[x][]) dfs2(son[x][]);
     else return;
 }
 ll md[N];
 int main()
 {
     judge();
     int n;read(n);init();rep(i,,n-)
     {
         int x,y,z;read(x);read(y);read(z);
         add_edge(x,y,z,i);add_edge(y,x,z,i);
         wod[i]=z;
     }fa[]=;dfs();int mj=;rep(i,,n) if(ma[i][]+ma[i][]>ma[mj][]+ma[mj][]) mj=i;
     rep(i,,n-) ans[i][]=ma[mj][]+ma[mj][];
     if(son[mj][])
     {
         dfs2(son[mj][]); for(int i=(int)tt.size()-;i>=;i--) Route.pb(tt[i]);
         for(int i=(int)tt2.size()-;i>=;i--) Rid.pb(tt2[i]); tt2.clear();tt.clear();
         Rid.pb(tp[son[mj][]]);
     }
     Route.pb(mj);
     if(son[mj][])
     {
         Rid.pb(tp[son[mj][]]);
         dfs2(son[mj][]); for(int i=;i<(int)tt.size();i++) Route.pb(tt[i]);
         for(int i=;i<(int)tt2.size();i++) Rid.pb(tt2[i]);
     }
     int sz=Route.size();memset(ma,,sizeof(ma));
     ll pre=;ll maa=;
     rep(i,,sz-)
     {
         int j=Route[i];
         Rep(xjt,j)
         {
             if(i && to[xjt]==Route[i-]) continue;
             if(i<sz- && to[xjt]==Route[i+]) continue;
             dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][]);
         }
         maa=max(maa,md[i]+pre);if(i!=sz-)ans[Rid[i]][]=maa;
         if(i!=sz-) pre+=wod[Rid[i]];
     }
     pre=; maa=;memset(md,,sizeof(md));
     per(i,sz-,)
     {
         int j=Route[i];
         Rep(xjt,j)
         {
             if(i && to[xjt]==Route[i-]) continue;
             if(i<sz- && to[xjt]==Route[i+]) continue;
             dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][]);
         }
         maa=max(maa,md[i]+pre);if(i)ans[Rid[i-]][]=maa;
         if(i) pre+=wod[Rid[i-]];
     }
     rep(i,,n-) if(ans[i][]>ans[i][]) swap(ans[i][],ans[i][]);
     ll solo=;
     rep(i,,n-)
     {
         solo+=ans[i][]*23333ll+ans[i][]*2333ll+233ll*(ll)i*(ll)i+23ll*(ll)i+2ll;
         //cerr<<ans[i][1]<<' '<<ans[i][0]<<endl;
         solo%=2333333333333333ll;
     }
     printf("%lld\n",solo);
     return ;
 }