YCOJ过河卒C++

过河卒是一道较简单 的问题，用递归或者动态规划都可以完成，但今天主要不是递归或者动态规划，而是用深度优先搜索做的。虽然会有两组TLE

深搜是一种向下搜索的算法（如图所示）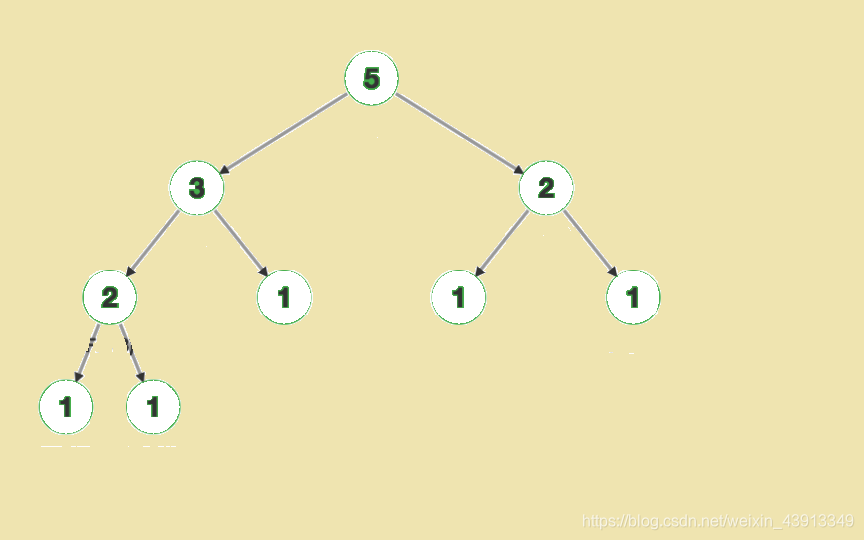

它能有效的统计中点到起点的所有路径，与BFS不同的是，BFS（广搜）是一层一层的搜索，而DFS（深搜）是往下搜，直到边界然后回溯，再搜另一边。所以，BFS用于找最短路，而DFS用于统计路径总数。

现在，再来看看过河卒的深搜思想。

Description

棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

Input

给出n、m和C点的坐标。

Output

从A点能够到达B点的路径的条数。

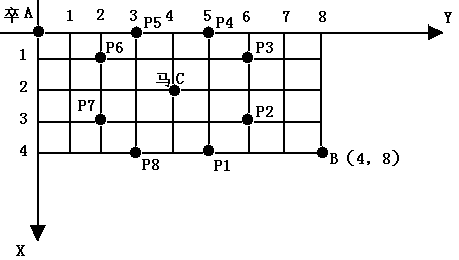
Sample Input 1

8 6 0 4

Sample Output 1

1617

——摘自YCOJ

首先，我们可以想到用两个二维数组来表示兵的行走方向和马的控制点。

兵的行走方向和马的控制点如图所示：



（蓝色代表卒以及行走方向，红色代表兵不能走的马的控制点，绿色代表中点）

于是，因为兵只能走两格，而马有八个控制点，所以，代码如下：

int dir[2][2] = {{1,0},{0,1}};
int die[8][2]={{-1,2},{-1,-2},{1,2},{1,-2},{2,-1},{-2,-1},{2,1},{-2,1}};

然后，卒要有边界值，便定义一个边界值：

bool in(int x,int y){
	return 0<=x && x<=n && 0<=y && y<=m;
}

现在，到了代码主体，DFS。当卒遇到了马，便应该向后回溯一步，再判断下一步（如图）

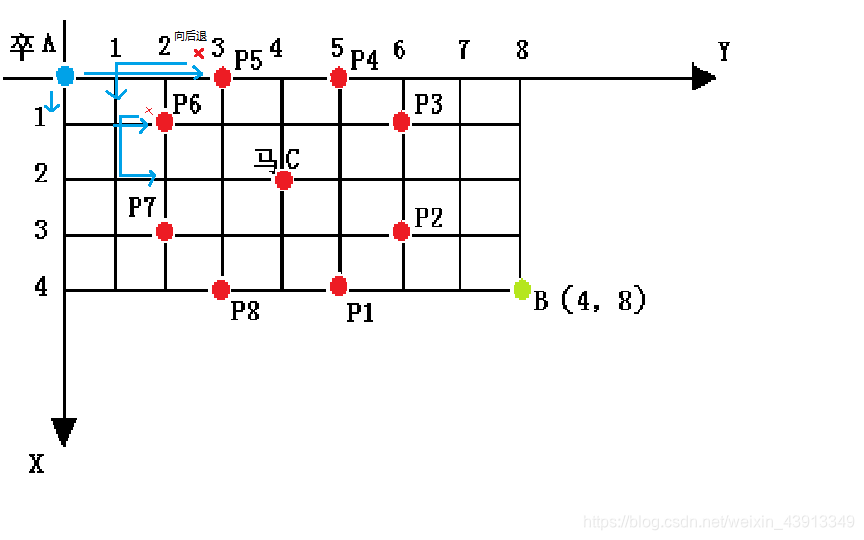
void  dfs(int x, int y){
	if(x == Tx&&y == Ty){
		sum++;//统计
		return ;
	}	

	for(int i=0;i<2;i++){
		int tx = x+dir[i][0];
		int ty = y+dir[i][1];
		if(in(tx, ty) && !mp[tx][ty] && !vis[tx][ty]){//判断马的控制点
			if(tx == Tx&& y == Ty){
				sum++;
			}else{
				vis[tx][ty]=1;//标记
				dfs(tx,ty);
				vis[tx][ty]=0;//解除标记
			}

		}
	}
}

深搜就这些了，但还有马的点和边界值：

for (int i=0;i<8;i++){
		int tx=x1+die[i][0];
		int ty=y1+die[i][1];
		if(in(tx,ty)){
			mp[tx][ty]=1;
		}
	}

最后上代码整体：
#include<bits/stdc++.h>
using namespace std;
bool mp[100][100];
bool vis[110][110];
int n,m;
int Sx,Sy ,Tx,Ty,sum = 0;
int dir[2][2] = {{1,0},{0,1}};
int die[8][2]={{-1,2},{-1,-2},{1,2},{1,-2},{2,-1},{-2,-1},{2,1},{-2,1}};
bool in(int x,int y){
	return 0<=x && x<=n && 0<=y && y<=m;
}

void  dfs(int x, int y){
	if(x == Tx&&y == Ty){
		sum++;
		return ;
	}	

	for(int i=0;i<2;i++){
		int tx = x+dir[i][0];
		int ty = y+dir[i][1];
		if(in(tx, ty) && !mp[tx][ty] && !vis[tx][ty]){
			if(tx == Tx&& y == Ty){
				sum++;
			}else{
				vis[tx][ty]=1;
				dfs(tx,ty);
				vis[tx][ty]=0;
			}

		}
	}
}

int main(){
	int x1,y1;
	cin >> n >> m>>x1>>y1;
	mp[x1][y1]=1;
	for (int i=0;i<8;i++){
		int tx=x1+die[i][0];
		int ty=y1+die[i][1];
		if(in(tx,ty)){
			mp[tx][ty]=1;
		}
	}
	Tx=n;
	Ty=m;
	vis[Sx][Sy] = 1;
 	dfs(Sx,Sy);
	cout <<sum;
	return 0;
}

但是，虽然样例过了，但会有两组TLE，所以得用到剪枝，但剪枝就不打了。DFS过河卒的整体思想就是这样的了。