清北考前刷题da5下午好

/*
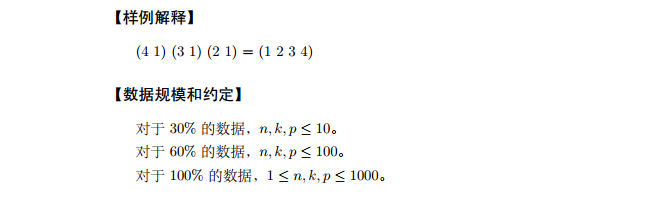
(4,1)*(3,1)*(2,1)的话1变成2然后一直是2
2变成1然后变成3
3变成1然后变成4
4变成1
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 1007

using namespace std;
int n,m,p,k,ans,cnt,tmp;
int a[N],pos[N];
struct node{
    int len,q[N];
}s[N];

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

int main()
{
    freopen("rotate.in","r",stdin);
    freopen("rotate.out","w",stdout);
    n=read();p=read();k=read();
    for(int i=;i<=n;i++) a[i]=i,pos[i]=i;
    for(int i=p;i>=;i--)
    {
        s[i].len=read();
        for(int j=;j<=s[i].len;j++) s[i].q[j]=read();
    }
    for(int i=;i<=p;i++)
    {
        for(int j=;j<=s[i].len;j++)
        {
            int x=s[i].q[j],y=s[i].q[];
            swap(a[pos[x]],a[pos[y]]);
            swap(pos[x],pos[y]);
        }
    }
    for(int i=;i<=n;i++) printf("%d ",a[i]);
    return ;
}

/*
60线段树
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

#define mod 1000000007
#define N 1003
#define ll long long

using namespace std;
int n,a,b,c,d,ans,cnt;
int And[N][N],Or[N][N];
int s[N];
struct tree{
    int l,r,sum1,sum2;
}tr[N<<];

bool cmp(int a,int b){return a>b;}

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

inline void pushup(int k)
{
    tr[k].sum1=tr[k<<].sum1 & tr[k<<|].sum1;
    tr[k].sum2=tr[k<<].sum2 | tr[k<<|].sum2;
}

void build(int k,int l,int r)
{
    tr[k].l=l;tr[k].r=r;
    if(l==r)
    {
        tr[k].sum1=read();
        tr[k].sum2=tr[k].sum1;
        return;
    }
    int mid=l+r>>;
    build(k<<,l,mid);build(k<<|,mid+,r);
    pushup(k);
}

int query1(int k,int l,int r)
{
    if(tr[k].l==l && tr[k].r==r) return tr[k].sum1;
    int mid=tr[k].l+tr[k].r>>;
    pushup(k);
    if(r<=mid) return query1(k<<,l,r);
    else if(l>mid) return query1(k<<|,l,r);
    else return query1(k<<,l,mid) & query1(k<<|,mid+,r);
}

int query2(int k,int l,int r)
{
    if(tr[k].l==l && tr[k].r==r) return tr[k].sum2;
    int mid=tr[k].l+tr[k].r>>;
    pushup(k);
    if(r<=mid) return query2(k<<,l,r);
    else if(l>mid) return query2(k<<|,l,r);
    else return query2(k<<,l,mid) | query2(k<<|,mid+,r);
}

int main()
{
    freopen("range.in","r",stdin);
    freopen("range.out","w",stdout);
    n=read();a=read();b=read();c=read();d=read();
    build(,,n);
    for(int i=;i<=n;i++)
      for(int j=i;j<=n;j++)
        And[i][j]=query1(,i,j),Or[i][j]=query2(,i,j);
    for(int i=;i<=n;i++)
      for(int j=i;j<=n;j++)
        if(And[i][j]<=b && And[i][j]>=a && Or[i][j]<=d && Or[i][j]>=c)
        {
            ans++;
            if(ans>mod) ans-=mod;
        }
    printf("%d\n",ans);
    return ;
} 

/*
有单调性
枚举左端点，二分右端点，ST表处理，计算答案。
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include <cmath>

#define N 100007
#define ll long long
#define mod 1000000007

using namespace std;
int n,a,b,c,d,ans;
int st1[N][],st2[N][];
int s[N];ll cnt;

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

int query1(int l,int r)
{
    int len=r-l+,p=log2(len);
    return st1[l][p] & st1[r-(<<p)+][p];
}

int query2(int l,int r)
{
    int len=r-l+,p=log2(len);
    return st2[l][p] | st2[r-(<<p)+][p];
}

int main()
{
    freopen("range.in","r",stdin);
    freopen("range.out","w",stdout);
    n=read();a=read();b=read();c=read();d=read();
    for(int i=;i<=n;i++)
      s[i]=read(),st1[i][]=st2[i][]=s[i];

    for(int j=;j<=;j++)
      for(int i=;i+(<<j)-<=n;i++)
        st1[i][j]=st1[i][j-] & st1[i+(<<(j-))][j-],
        st2[i][j]=st2[i][j-] | st2[i+(<<(j-))][j-];

    int sum1,sum2,L,R,mid;ans=,cnt=;
    for(int i=;i<=n;i++)
    {
        sum1=sum2=s[i];
        for(int j=i;j<=n;j++)
        {
            sum1=query1(i,j);sum2=query2(i,j);
            L=j,R=n+;
            while(L<=R)
            {
                mid=L+R>>;
                if(query1(i,mid)==sum1 && query2(i,mid)==sum2) ans=mid,L=mid+;
                else R=mid-;
            }
            if(a<=sum1 && sum1<=b && c<=sum2 && sum2<=d) cnt+=ans-j+;j=ans;
        }
    }
    printf("%I64d\n",cnt%mod);
    return ;
}

/*
不先考虑k个，1~n先都考虑。
按子树为单位树形dp
f[x][j]表示以x为根的子树有j个果子方案数。
x显然果子必须拿，其他的果子需要分配。
但如果有很多孩子，那么挨个分配会T。
所以考虑树形dp常用策略把子树编号。
考虑孩子的每个前缀分多少，还剩多少。
就是每个前缀的max而不是子集的max。
所以要设计前缀的状态：g[i][j]表示以i为结尾的前缀分j个果子的方案数。
就转化为了背包问题。
但直接转移是n^3的，考虑优化。
可以看出枚举每个前缀是不必要的。
从根节点递归到子节点往上反的时候子节点的状态先继承父节点的状态，然后进行转移。
这样每个点都会从左到右把它儿子的每个前缀计算答案并取max。详见代码。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define mod 1000000007
#define N 1007
#define ll long long

using namespace std;
int n,m,ans,cnt;
ll f[N][N],p[N];
int val[N],head[N];
struct edge{
    int u,v,net;
}e[N<<];

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

inline void add(int u,int v)
{
    e[++cnt].v=v;e[cnt].net=head[u];head[u]=cnt;
}

int dp(int u,int fa)
{
    int siz=;
    for(int i=head[u];i;i=e[i].net)
    {
        int v=e[i].v;
        if(v==fa) continue;
        for(int j=;j<=n-val[v];j++) f[v][j+val[v]]=f[u][j];
        int tmp=dp(v,u);
        for(int j=;j<=n;j++)
          f[u][j]=(p[tmp-]*f[u][j]%mod+f[v][j])%mod;
        siz+=tmp;
    }return siz;
}

int main()
{
    int x,y,z;
    n=read();m=read();p[]=;
    for(int i=;i<=n;i++)p[i]=(p[i-]*)%mod;
    for(int i=;i<=n;i++) val[i]=read();
    for(int i=;i<n;i++)
    {
        x=read();y=read();
        add(x,y);add(y,x);
    }
    f[][val[]]=;dp(,);
    printf("%d\n",int(f[][m]));
    return ;
}