Codeforces Round #272 (Div. 2) D.Dreamoon and Sets 找规律

D. Dreamoon and Sets

 

Dreamoon likes to play with sets, integers and 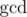.  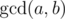is defined as the largest positive integer that divides both a and b.

Let S be a set of exactly four distinct integers greater than 0. Define S to be of rank k if and only if for all pairs of distinct elements si, sjfrom S, .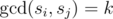

Given k and n, Dreamoon wants to make up n sets of rank k using integers from 1 to m such that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum m that makes it possible and print one possible solution.

Input

The single line of the input contains two space separated integers n, k (1 ≤ n ≤ 10 000, 1 ≤ k ≤ 100).

Output

On the first line print a single integer — the minimal possible m.

On each of the next n lines print four space separated integers representing the i-th set.

Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal m, print any one of them.

Sample test(s)

input

1 1

output

5
1 2 3 5

Note

For the first example it's easy to see that set {1, 2, 3, 4} isn't a valid set of rank 1 since .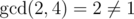

题意：求出n个集合均为4个元素，且每个集合内任意两两，元素的最大公约数为k，集合不允许有交集，当n*4个元素最大值最小时，输出所有n个集合，

题解：我是暴力水过去的，正解是：

两两元素之间是互质的，然后为了满足元素最大值最小，

在除掉k后，任意集合内肯定是由3个奇数，1个偶数组成，

因为若少一个奇数，就会有至少一对数不互质，

若多一个奇数，元素最大值就会变大。

所以，从1开始构建所有元素集合即可。

#include<iostream>
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
int main()
{
    int n,k;
    cin>>n>>k;
    cout<<(*n-)*k<<endl;
    while(n--)
    {
        cout<<(*n+)*k<<" "<<(*n+)*k<<" "<<(*n+)*k<<" "<<(*n+)*k<<endl;
    }
}

正解代码

///
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll;
#define mem(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,127,sizeof(a));
#define TS printf("111111\n");
#define FOR(i,a,b) for( int i=a;i<=b;i++)
#define FORJ(i,a,b) for(int i=a;i>=b;i--)
#define READ(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define inf 100000000
inline ll read()
{
    ll x=,f=;
    char ch=getchar();
    while(ch<''||ch>'')
    {
        if(ch=='-')f=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=x*+ch-'';
        ch=getchar();
    }
    return x*f;
}
//****************************************
///****************************************************************
/// Miller_Rabin 算法进行素数测试
///速度快，而且可以判断 <2^63的数
//****************************************************************
const int S=;///随机算法判定次数，S越大，判错概率越小

///计算 (a*b)%c.   a,b都是long long的数，直接相乘可能溢出的
///  a,b,c <2^63
long long mult_mod(long long a,long long b,long long c)
{
    a%=c;
    b%=c;
    long long ret=;
    while(b)
    {
        if(b&){ret+=a;ret%=c;}
        a<<=;
        if(a>=c)a%=c;
        b>>=;
    }
    return ret;
}

///计算  x^n %c
long long pow_mod(long long x,long long n,long long mod)//x^n%c
{
    if(n==)return x%mod;
    x%=mod;
    long long tmp=x;
    long long ret=;
    while(n)
    {
        if(n&) ret=mult_mod(ret,tmp,mod);
        tmp=mult_mod(tmp,tmp,mod);
        n>>=;
    }
    return ret;
}

///以a为基,n-1=x*2^t      a^(n-1)=1(mod n)  验证n是不是合数
///一定是合数返回true,不一定返回false
bool check(long long a,long long n,long long x,long long t)
{
    long long ret=pow_mod(a,x,n);
    long long last=ret;
    for(int i=;i<=t;i++)
    {
        ret=mult_mod(ret,ret,n);
        if(ret==&&last!=&&last!=n-) return true;//合数
        last=ret;
    }
    if(ret!=) return true;
    return false;
}

/// Miller_Rabin()算法素数判定
///是素数返回true.(可能是伪素数，但概率极小)
///合数返回false;

bool Miller_Rabin(long long n)
{
    if(n<)return false;
    if(n==)return true;
    if((n&)==) return false;//偶数
    long long x=n-;
    long long t=;
    while((x&)==){x>>=;t++;}
    for(int i=;i<S;i++)
    {
        long long a=rand()%(n-)+;///rand()需要stdlib.h头文件
        if(check(a,n,x,t))
            return false;//合数
    }
    return true;
}

#define maxn 100000+5
int a[maxn],n,m;
vector<int >G;
int gcd(int M,int N )
{
    int Rem;
    while( N >  )
    {
        Rem = M % N;
        M = N;
        N = Rem;
}
    return M;
}
int main(){
   n=read(),m=read();
    int ans[maxn];
     int k=;
     int tmp=;
     G.clear();
     for(int i=;i<=n;i++){
            while(G.size()!=){
                    bool flag=;
                 for(int j=;j<G.size();j++){
                if(gcd(G[j],m*tmp)!=m)flag=;
                 }
                if(flag) G.push_back(tmp*m);
                tmp++;
            }
              for(int j=;j<G.size();j++)
                   a[++k]=G[j];
                   G.clear();
          if(!Miller_Rabin(tmp))tmp++;
     }
     cout<<a[k]<<endl;
     for(int i=;i<=k;i+=){
         cout<<a[i]<<" "<<a[i+]<<" "<<a[i+]<<" "<<a[i+]<<endl;
     }

  return ;
}

暴力代码