JZOJ 5461 购物 —— 贪心

题目：https://jzoj.net/senior/#main/show/5461

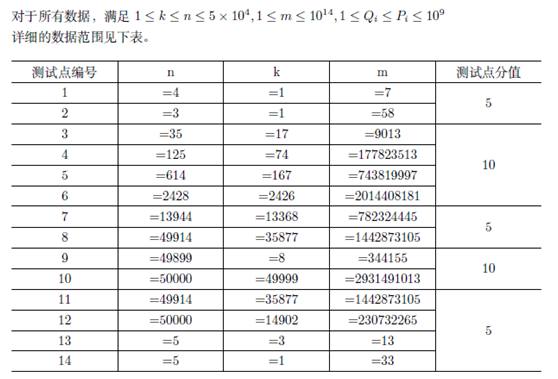
贪心，原来想了个思路，优先选优惠价最小的 K 个，然后其他按原价排序遍历；

如果当前物品没选过，原价选上，如果选过，考虑把它换成原价，然后把优惠价最小的下一个选上；

但这样做是75分，没考虑 替换没选过的物品 和 比较替换后是否更优；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
int const maxn=5e4+;
int n,K,cnt;
ll m,ans;
bool vis[maxn];
struct N{
    int w,t,id;
    bool operator < (const N &y) const
        {return w>y.w;}
}p[maxn];
priority_queue<N>q;
bool cmp(N x,N y){return x.t<y.t;}
int main()
{
    freopen("shopping.in","r",stdin);
    freopen("shopping.out","w",stdout);
    scanf("%d%d%lld",&n,&K,&m);
    for(int i=;i<=n;i++)scanf("%d%d",&p[i].w,&p[i].t);
    sort(p+,p+n+,cmp);
    for(int i=;i<=n;i++)p[i].id=i,q.push(p[i]);
    for(int i=;i<=K&&i<=n;i++)
    {
        if(ans+p[i].t>m)break;
        vis[i]=; cnt=i; ans+=p[i].t;
    }
    if(cnt==n){printf("%d\n",n); return ;}
    while(q.size())
    {
        int x=q.top().id,w=q.top().w,t=q.top().t; q.pop();
        if(!vis[x])
        {
            if(ans+w>m)continue;
            ans+=w; cnt++;
        }
        else
        {
            if(ans-p[x].t+p[x].w+p[K+].t>m)continue;
            ans=ans-p[x].t+p[x].w+p[K+].t; K++; cnt++;
            vis[x]=; vis[K]=;
        }
    }
    printf("%d\n",cnt);
    return ;
}

原

正解是直接把选中物品的 原价 - 优惠价 放入小根堆，然后其他物品按原价排序，直接判断、替换；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
int const maxn=5e4+;
int n,K,cnt;
ll m,ans;
bool vis[maxn];
struct N{int w,t,id;}p[maxn];
priority_queue<int>q;
bool cmp(N x,N y){return x.t<y.t;}
bool cmp2(N x,N y){return x.w<y.w;}
int main()
{
//    freopen("shopping.in","r",stdin);
//    freopen("shopping.out","w",stdout);
    scanf("%d%d%lld",&n,&K,&m);
    for(int i=;i<=n;i++)scanf("%d%d",&p[i].w,&p[i].t),p[i].id=i;
    sort(p+,p+n+,cmp);
    for(int i=;i<=K&&i<=n;i++)
    {
        if(ans+p[i].t>m)break;
        cnt=i; ans+=p[i].t;
        q.push(p[i].t-p[i].w); vis[p[i].id]=;
    }
    if(cnt==n){printf("%d\n",n); return ;}
    sort(p+,p+n+,cmp2);
    for(int i=,x;i<=n;i++)
    {
        if(vis[p[i].id])continue;
        if(q.size())
        {
            x=-q.top();
            if(x+p[i].t>p[i].w&&ans+p[i].w<=m)ans+=p[i].w,cnt++;
            else if(x+p[i].t<=p[i].w&&ans+x+p[i].t<=m)ans+=x+p[i].t,cnt++,q.pop(),q.push(p[i].t-p[i].w);
        }
        else if(ans+p[i].w<=m)ans+=p[i].w,cnt++;
    }
    printf("%d\n",cnt);
    return ;
}

TJ

但这样总感觉不对，因为按原价排序并不能保证替换最优；

这里就是反例：

6 3 15

10 3

8 4

7 5

5 1

4 2

3 2

按这样的做法，会先选后3个物品，然后按 1,2,3 把前三个物品排序；

然后把物品6换成原价购买，优惠价购买物品 3；

之后就不能买了，输出4；

但实际上应该是优惠价购买物品 1,2,4，原价购买物品 5,6，答案是5；

所以应该采用别的贪心策略，看到了一种很好的：https://blog.csdn.net/qq_40448823/article/details/81488195 (不过这篇博客贴错题面了囧)

所有物品都按优惠价排序，同时开了一个原价购买的大根堆，存已经原价买下的东西的原价；

先买 K 个优惠价的，然后从优惠价排序的顺序继续往后看，每次去掉优惠买中 原价 - 优惠价 最小的一个，优惠价买下一个；

然后回头看看能否原价买上去掉的这个东西，能就原价买上，不能就去原价物品堆里看看，如果能替换一下使花钱更少，那么就替换一下；

而如果优惠价购买下一个不如原价购买下一个优，那么原价购买下一个，同样进行替换的判断；

然后就能过掉上面的数据了，主要是因为优惠价部分排序满足，原价部分用大根堆替换来满足；

不过数据太水，也不知道这个做法是否完美无瑕，看样子应该没问题，先放到这里吧。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
int const maxn=;
int n,K,ans;
ll sum,m;
struct N{
    int w,t,c;
    bool operator < (const N &y) const
        {return c>y.c;}
}p[maxn];
priority_queue<N>Q;
priority_queue<int>q;
bool cmp(N x,N y){return x.t<y.t;}
int main()
{
    freopen("shopping.in","r",stdin);
    freopen("shopping.out","w",stdout);
    scanf("%d%d%lld",&n,&K,&m);
    for(int i=;i<=n;i++)scanf("%d%d",&p[i].w,&p[i].t),p[i].c=p[i].w-p[i].t;
    sort(p+,p+n+,cmp);
    for(int i=;i<=n;i++)
    {
        if(Q.size()<K&&sum+p[i].t<=m){sum+=p[i].t; ans++; Q.push(p[i]);}//Q是按差价排序的堆
        else if(Q.size()==K)//其他物品是按优惠价排序的
        {
            N x=Q.top();
            if(x.c+p[i].t<=p[i].w)//优惠价购买较优
            {
                Q.pop(); Q.push(p[i]);
                sum=sum-x.t+p[i].t;//先优惠价买上
                if(sum+x.w<=m){sum+=x.w; ans++; q.push(x.w);}//可以原价买原来那个 //q是原价购买了的堆
                else if(q.size()&&q.top()>x.w){sum=sum-q.top()+x.w; q.pop(); q.push(x.w);}
                //不能买了，换掉之前原价购买的一个物品，可以更优
            }
            else if(sum+p[i].w<=m){sum+=p[i].w; ans++; q.push(p[i].w);}//原价购买
            else if(q.size()&&q.top()>p[i].w){sum=sum-q.top()+x.w; q.pop(); q.push(x.w);}//不能买了，替换更优
        }
    }
    printf("%d\n",ans);
    return ;
}