bzoj3995

线段树

额 计蒜客竟然把这个出成noip模拟题。。。

这个东西很像1018，只不过维护的东西不太一样

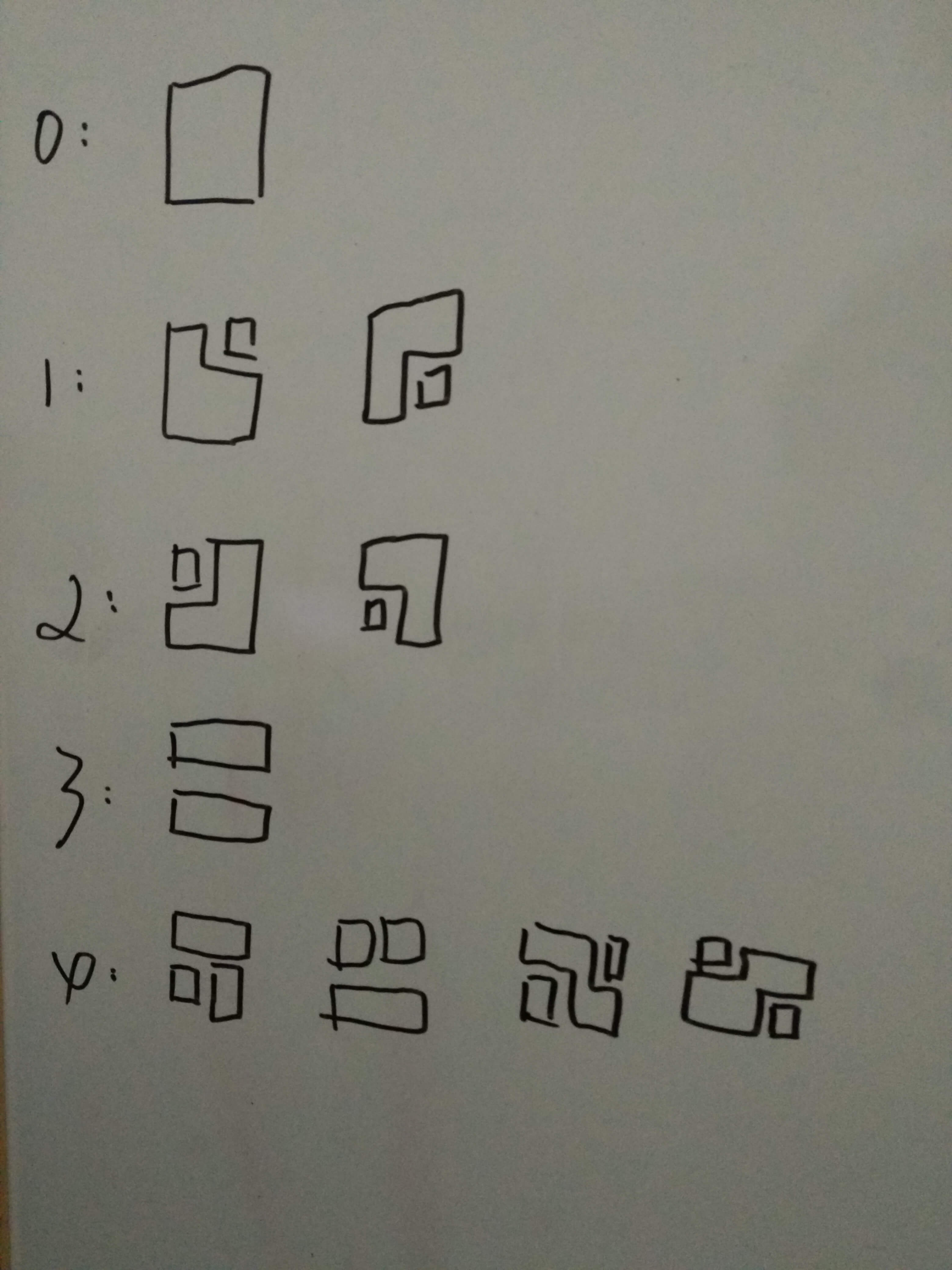
具体有这五种情况，合并请看代码，自己写了一个结果wa了，然后就copy了一下。。。

然后build的时候不用把叶子结点的值赋成inf，感觉奥妙重重

#include<bits/stdc++.h>
using namespace std;
const int N = ;
int n, m;
int tree[N << ][], a[N], b[N], c[N], ans[];
void up(int &a, const int &b) { a = min(a, b); } /*
void maintain(int a[5], int l[5], int r[5], int mn, int sm)
{
    memset(a, 0x3f3f3f3f, sizeof(tree[0]));
    up(a[0], l[0] + r[0] + mn);
    up(a[0], l[0] + r[3] + sm);
    up(a[0], l[3] + r[0] + sm);
    up(a[0], l[1] + r[0] + sm);
    up(a[0], l[0] + r[2] + sm);
    up(a[1], l[0] + r[1] + mn);
    up(a[1], l[3] + r[1] + sm);
    up(a[1], l[0] + r[4] + sm);
    up(a[1], l[0] + r[3] + mn);
    up(a[1], l[0] + r[4] + mn);
    up(a[1], l[0] + r[2] + mn);
    up(a[2], l[2] + r[0] + mn);
    up(a[2], l[4] + r[0] + sm);
    up(a[2], l[3] + a[0] + mn);
    up(a[2], l[1] + r[0] + mn);
    up(a[2], l[2] + r[3] + sm);
    up(a[2], l[2] + r[2] + sm);
    up(a[3], l[3] + r[3] + sm);
    up(a[4], l[2] + r[1] + mn);
    up(a[4], l[2] + r[3] + mn);
    up(a[4], l[2] + r[4] + sm);
    up(a[4], l[3] + r[1] + mn);
    up(a[4], l[3] + r[4] + sm);
    up(a[4], l[2] + r[1] + mn);
    up(a[4], l[4] + r[3] + sm);
    up(a[4], l[4] + r[1] + sm);
    up(a[4], l[3] + r[3] + mn);
} */
void maintain(int a[] , int l[] , int r[] , int mn , int sm)
{
    memset(a , 0x3f3f , sizeof(tree[]));

    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);

    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);

    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);    

    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + mn);
    up(a[] , l[] + r[] + sm);

    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
    up(a[] , l[] + r[] + sm);
}

void build(int l, int r, int o)
{
    if(l == r)
    {
        tree[o][] = c[l];
//      tree[o][1] = tree[o][2] = 0x3f3f3f3f;
        return;
    }
    int mid = (l + r) >> ;
    build(l, mid, o << );
    build(mid + , r, o <<  | );
    int mn = min(a[mid], b[mid]), sm = a[mid] + b[mid];
    maintain(tree[o], tree[o << ], tree[o <<  | ], mn, sm);
//  printf("l = %d r = %d\n", l, r);
//  for(int i = 0; i < 5; ++i) printf("tree[%d][%d] = %d\n", o, i, tree[o][i]);
}
void update(int l, int r, int o, int pos)
{
    if(l == r)
    {
        tree[o][] = c[l];
        return;
    }
    int mid = (l + r) >> ;
    if(pos <= mid) update(l, mid, o << , pos);
    else update(mid + , r, o <<  | , pos);
    int mn = min(a[mid], b[mid]), sm = a[mid] + b[mid];
    maintain(tree[o], tree[o << ], tree[o <<  | ], mn, sm);
}
bool query(int l, int r, int o, int la, int lb, int tmp[])
{
    if(l > lb || r < la) return false;
    if(l >= la && r <= lb)
    {
        for(int i = ; i < ; ++i) tmp[i] = tree[o][i];
        return true;
    }
    int mid = (l + r) >> , tmp1[], tmp2[];
    bool flag1 = query(l, mid, o << , la, lb, tmp1);
    bool flag2 = query(mid + , r, o <<  | , la, lb, tmp2);
    if(flag1 && flag2)
    {
        int mn = min(a[mid], b[mid]), sm = a[mid] + b[mid];
        maintain(tmp, tmp1, tmp2, mn, sm);
        return true;
    }
    if(flag1)
    {
        for(int i = ; i < ; ++i) tmp[i] = tmp1[i];
        return true;
    }
    if(flag2)
    {
        for(int i = ; i < ; ++i) tmp[i] = tmp2[i];
        return true;
    }
    return false;
}
int main()
{
    cin >> n >> m;
    for(int i = ; i < n; ++i) scanf("%d", &a[i]);
    for(int i = ; i < n; ++i) scanf("%d", &b[i]);
    for(int i = ; i <= n; ++i) scanf("%d", &c[i]);
    build(, n, );
    while(m--)
    {
        int x0, x1, y0, y1, w;
        char opt[];
        scanf("%s", opt);
        if(opt[] == 'C')
        {
            scanf("%d%d%d%d%d", &x0, &y0, &x1, &y1, &w);
            if(x0 == x1)
            {
                if(y0 > y1) swap(y0, y1);
                if(x0 == ) a[y0] = w;
                if(x0 == ) b[y0] = w;
                update(, n, , y0);
                update(, n, , y1);
            }
            if(y0 == y1)
            {
                c[y0] = w;
                update(, n, , y0);
            }
        }
        if(opt[] == 'Q')
        {
            scanf("%d%d", &y0, &y1);
            query(, n, , y0, y1, ans);
            printf("%d\n", ans[]);
        }
    }
    return ;
}