Camelot_floyd&&DP

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3119		Accepted: 1455

Description

Centuries ago, King Arthur and the Knights of the Round Table used to meet every year on New Year's Day to celebrate their fellowship. In remembrance of these events, we consider a board game for one player, on which one king and several knight pieces are placed at random on distinct squares. 
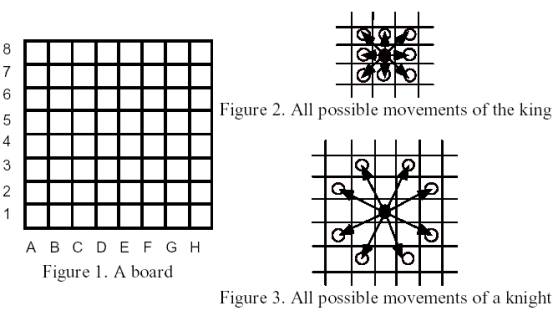
The Board is an 8x8 array of squares. The King can move to any adjacent square, as shown in Figure 2, as long as it does not fall off the board. A Knight can jump as shown in Figure 3, as long as it does not fall off the board. 

During the play, the player can place more than one piece in the same square. The board squares are assumed big enough so that a piece is never an obstacle for other piece to move freely. 
The player's goal is to move the pieces so as to gather them all in the same square, in the smallest possible number of moves. To achieve this, he must move the pieces as prescribed above. Additionally, whenever the king and one or more knights are placed in the same square, the player may choose to move the king and one of the knights together henceforth, as a single knight, up to the final gathering point. Moving the knight together with the king counts as a single move.

Write a program to compute the minimum number of moves the player must perform to produce the gathering.

Input

Your program is to read from standard input. The input contains the initial board configuration, encoded as a character string. The string contains a sequence of up to 64 distinct board positions, being the first one the position of the king and the remaining ones those of the knights. Each position is a letter-digit pair. The letter indicates the horizontal board coordinate, the digit indicates the vertical board coordinate.

0 <= number of knights <= 63

Output

Your program is to write to standard output. The output must contain a single line with an integer indicating the minimum number of moves the player must perform to produce the gathering.

Sample Input

D4A3A8H1H8

Sample Output

10

【题意】有一个国王和n个骑士在一个8*8的棋盘里，国王可以往邻近的8个点走，骑士走日字姓，问最后都走到同一个格子需要几步，其中国王一旦与一个骑士相遇之后，他们就是一个整体，按骑士的方法来移动。

【思路】先求出棋盘上任意一格到另一格的国王走法和骑士走法的最少步数存储在两个二维数组中，每格的表示方法i*8+j;

再假设国王与一个骑士在j格相遇，所有人集合在i，tmp=min（tmp,sum-knight[hh[k]][i]+knight[hh[k]][j]+knight[j][i]）;

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int inf=0x3f3f3f3f;
const int N=;
const int di1[][] = {,,,,-,,,-,,,,-,-,,-,-};
const int di2[][] = {,,,,,-,,-,-,,-,,-,-,-,-};
int king[][],knight[][];
void floyd()
{
    for(int k=;k<;k++)
    {
        for(int i=;i<;i++)
        {
            for(int j=;j<;j++)
            {
                king[i][j]=min(king[i][j],king[i][k]+king[k][j]);
                knight[i][j]=min(knight[i][j],knight[i][k]+knight[k][j]);
            }
        }
    }
}
void init()//求出棋盘上任意一格到另一格的最短路径
{
    memset(king,inf,sizeof(king));
    memset(knight,inf,sizeof(knight));
    for(int i=;i<;i++)
        king[i][i]=knight[i][i]=;
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
        {
            for(int k=;k<;k++)
            {
                int x1=i+di1[k][];
                int y1=j+di1[k][];
                int x2=i+di2[k][];
                int y2=j+di2[k][];
                if(x1>=&&x1<&&y1>=&&y1<)
                    king[i*+j][x1*+y1]=;
                if(x2>=&&x2<&&y2>=&&y2<)
                    knight[i*+j][x2*+y2]=;
            }
        }
    }
    floyd();
}
int main()
{
    char str[];
    int hh[],kk,ans;
    init();
    while(~scanf("%s",str))
    {
        int len=strlen(str);
        int cnt=;
        ans=inf;
        kk=(str[]-'A')*+(str[]-'');//坐标用这种方法记录，这样开一个二维数组就可以搞定了
        for(int i=;i<len;i+=)
            hh[cnt++]=(str[i]-'A')*+(str[i+]-'');
        int sum,tmp;
        for(int i=;i<;i++)
        {
            for(int j=;j<;j++)
            {
                sum=king[kk][j];//king与一个骑士在j这一格相遇了
                for(int k=;k<cnt;k++)
                {
                    sum+=knight[hh[k]][i];//所有骑士集合在i；
                }
                tmp=inf;
                for(int k=;k<cnt;k++)
                {
                    tmp=min(tmp,sum-knight[hh[k]][i]+knight[hh[k]][j]+knight[j][i]);//找出最初与国王相遇的骑士，使终点为i时的步数最小
                    ans=min(tmp,ans);
                }
            }
        }
        cout<<ans<<endl;
    }
    return ;
}