V-rep学习笔记：机器人逆运动学数值解法（Cyclic Coordinate Descent Method）

　　When performing inverse kinematics (IK) on a complicated bone chain, it can become too complex for an analytical solution. Cyclic Coordinate Descent (CCD) is an alternative that is both easy to implement and efficient to process。逆运动学问题一般采用解析法和基于Jacobian矩阵的迭代方法，前者虽然精度高而且能达到实时的效果，但是随着关节的增多，自由度随着增多，数学建模也变得很困难，甚至不可解。而后者很难达到实时的效果。

CCD 算法的思想

　　Cyclic Coordinate Descent (CCD) 是一个启发式的迭代搜索算法，它通过每一次只改变一个关节的参数来逐步减少位置误差和姿态误差，每个迭代过程包括一个从关节链结构的末端到基点的遍历过程。由于CCD 方法将多关节的关节链问题简化为单关节问题，可以用解析法处理，因此每一步的迭代可以相当快。当求得每个关节的参数 (转角)θ后，将其代入正向运动学方程求得末端效器和每个关节的位置。从运动链的末端开始 , 逐步改变每个关节的旋转角度。先是改变最末端的关节，末端关节到末段执行器的向量为图中蓝色线段，末端关节到目标点的向量为图中红色线段。求出 2 个向量的夹角α，让末端关节下的子链绕旋转轴转α角度，则末端执行器达到一个新位置。若没有达到目标，则继续取当前关节的上一关节，改变其旋转角度，直到选到根节点。若末端还没有达到目标位置，则又从末端关节开始新一轮运动，直到位置误差足够小或者到达了给定的循环次数。

　　After our first loop through the bone chain, we have moved the end effector much closer to the target position. By repeating this process, we will continue to get closer and closer. Once we have reached a tolerable distance from the target position or once we have performed too many iterations (for performance reasons), we can stop looping.下面三幅图展示了CCD算法的3次迭代过程，可以看出随着迭代的进行，末端离目标点越来越近。

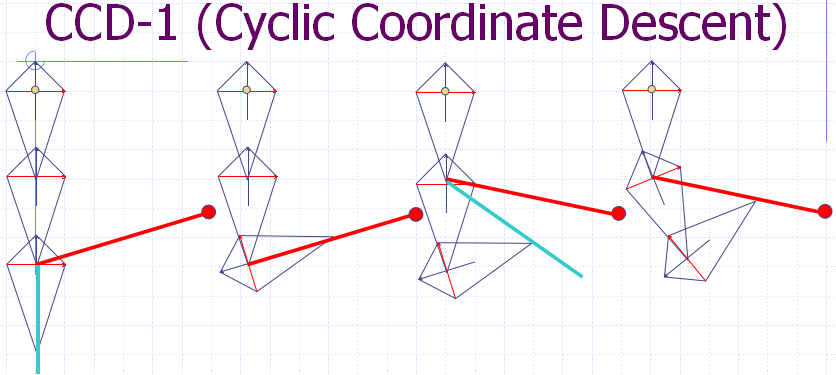
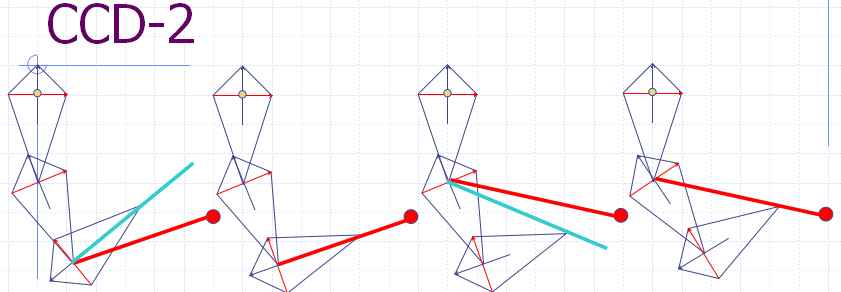
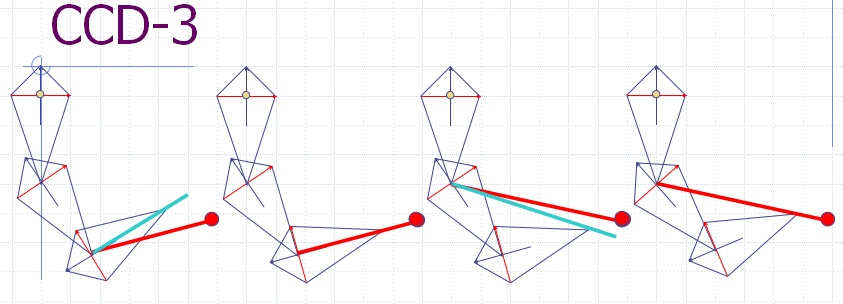
下面在V-rep中建立平面3连杆机构，各杆长均为0.5m，使用Python脚本计算运动学逆解并控制V-rep中的模型，使其达到目标位置。

# -*- coding: utf-8 -*-
import vrep             # V-rep library
import sys
import time
import math  

# This function will convert an angle to the equivalent rotation in the range [-pi,pi]
def ConfineAngle(angle):
    angle = angle % (2.0 * math.pi)
    if( angle < -math.pi ):
        angle += (2.0 * math.pi)
    if( angle > math.pi ):
        angle -= (2.0 * math.pi)
    return angle

def CalcIK():
    id = linkNum - 1
    while id >= 0:
        retcode, J_pos = vrep.simxGetObjectPosition(clientID,joint_handle[id],-1,vrep.simx_opmode_oneshot_wait)
        retcode, tip = vrep.simxGetObjectPosition(clientID,tip_handle, -1, vrep.simx_opmode_oneshot_wait)

        # Get the vector from the current bone to the end effector position.
        curToEndX = tip[0] - J_pos[0]
        curToEndY = tip[1] - J_pos[1]
        curToEndMag = math.sqrt( curToEndX*curToEndX + curToEndY*curToEndY )

        # Get the vector from the current bone to the target position.
        curToTargetX = target[0] - J_pos[0];
        curToTargetY = target[1] - J_pos[1];
        curToTargetMag = math.sqrt(curToTargetX*curToTargetX+curToTargetY*curToTargetY)

        # Get rotation
        endTargetMag = curToEndMag*curToTargetMag
        if endTargetMag <= 0.0001:    # prevent division by small numbers
            cosRotAng = 1
            sinRotAng = 0
        else:
            cosRotAng = (curToEndX*curToTargetX + curToEndY*curToTargetY) / endTargetMag
            sinRotAng = (curToEndX*curToTargetY - curToEndY*curToTargetX) / endTargetMag

        # Clamp the cosine into range when computing the angle(might be out of rangedue to floating point error)
        rotAng = math.acos(max(-1, min(1,cosRotAng)))
        if  sinRotAng < 0.0:
            rotAng = -rotAng

        q[id] = q[id] + rotAng

        # Rotate the current link
        if(id == 0):
            vrep.simxSetJointPosition(clientID,joint_handle[id], ConfineAngle(q[id])+math.pi/2, vrep.simx_opmode_oneshot)
        else:
            vrep.simxSetJointPosition(clientID,joint_handle[id], ConfineAngle(q[id]), vrep.simx_opmode_oneshot)

        # Check for termination
        retcode, tip = vrep.simxGetObjectPosition(clientID,tip_handle, -1, vrep.simx_opmode_oneshot_wait)
        endToTargetX = (target[0] - tip[0])
        endToTargetY = (target[1] - tip[1])
        error = math.sqrt(endToTargetX*endToTargetX + endToTargetY*endToTargetY)
        if( error <= stol ):
            # We found a valid solution.
            return 1, error
        id = id - 1

    return 0, error  # cannot get to the target in this iteration

if __name__ == "__main__":
    # Starts a communication thread with the server
    clientID = vrep.simxStart('127.0.0.1', 20001, True, True, 5000, 5)

    # clientID: the client ID, or -1 if the connection to the server was not possible
    if clientID != -1:  #check if client connection successful
        print 'Connected to remote API server'
    else:
        print 'Connection not successful'
        sys.exit('Could not connect')    # Exit from Python

    # Retrieves an object handle based on its name.
    errorCode,tip_handle = vrep.simxGetObjectHandle(clientID,'tip',vrep.simx_opmode_oneshot_wait)
    errorCode,target_handle = vrep.simxGetObjectHandle(clientID,'target',vrep.simx_opmode_oneshot_wait)
    errorCode,consoleHandle = vrep.simxAuxiliaryConsoleOpen(clientID,'info',4,1+4,None,None,None,None,vrep.simx_opmode_oneshot_wait)
    joint_handle = [-1,-1,-1]    # store the joint handles
    for i in range(3):
        errorCode,joint_handle[i] = vrep.simxGetObjectHandle(clientID,'j'+str(i+1),vrep.simx_opmode_oneshot_wait)

    ilimit = 100    # maximum iteration
    stol = 1e-2     # tolerance
    q = [0,0,0]     # initial joint value
    linkNum = 3     # number of links

    retcode, target = vrep.simxGetObjectPosition(clientID,target_handle, -1, vrep.simx_opmode_oneshot_wait)
    retcode, tip = vrep.simxGetObjectPosition(clientID,tip_handle, -1, vrep.simx_opmode_oneshot_wait)

    count = 0
    isOK = 0
    while ( not isOK ):
        isOK,err = CalcIK()

        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,None,vrep.simx_opmode_oneshot_wait)
        count = count + 1
        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,str(count)+' iterations err:'+str(err),vrep.simx_opmode_oneshot_wait)   

        if count > ilimit:
            vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,"Solution wouldn't converge\r\n",vrep.simx_opmode_oneshot_wait)
            break
        #time.sleep(0.1)

    # Ends the communication thread. This should be the very last remote API function called on the client side
    vrep.simxFinish(clientID)

　　点击仿真按钮并运行Python控制脚本后，可以看到V-rep中的连杆模型不断调整其关节角，同时误差err逐渐减小。当误差减小到一定程度，就可以停止迭代。下面三幅图中目标处于不同位置，可以发现目标位置对迭代次数有较大的影响（为什么会这样？）

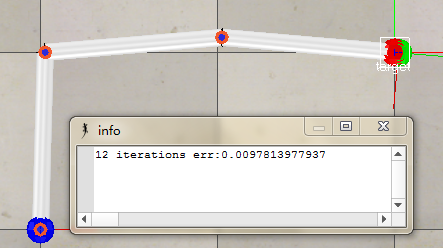
参考：

1.Cyclic Coordinate Descent in 2D ：http://www.ryanjuckett.com/programming/cyclic-coordinate-descent-in-2d/

2. 阳小涛 ,杨克俭. CCD 算法及其在逆运动学中的应用与实现[J]. 重 庆 工 学 院 学 报 (自然科学),2008 年 5 月