详解使用 Tarjan 求 LCA 问题（图解）

LCA问题有多种求法，例如倍增，Tarjan。

本篇博文讲解如何使用Tarjan求LCA。

如果你还不知道什么是LCA，没关系，本文会详细解释。

在本文中，因为我懒为方便理解，使用二叉树进行示范。

LCA是什么，能吃吗?

LCA是树上最近公共祖先问题。

最近公共祖先就是树上有两个结点，找一个结点，是他们的公共祖先，并且离他们两个结点最近。

例如这是一棵树：

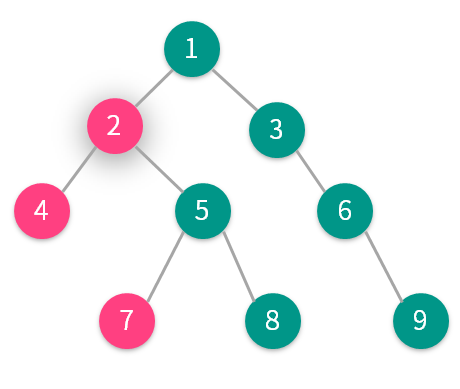
树上 4,7 两个结点的 LCA 就是 2 了。

1 虽然也是他们的公共祖先，但并不是最近的。

再举个例子，8,5 的祖先是 5。8,6 的祖先是 1。

怎么求LCA问题？

在开头已经说过了，LCA 问题有多种求法。本文要介绍的是相对简单的 Tarjan 求 LCA。

注意：Tarjan 求 LCA 是一种离线的算法，也就是说它一遍求出所有需要求的点的 LCA，而不是需要求哪两个点再去求。

在开始介绍前的补充

Tarjan 求 LCA 需要用到并查集，以下是本人使用的并查集模板。

int fa[100000];
void reset(){
	for (int i=1;i<=100000;i++){
		fa[i]=i;
	}
}
int getfa(int x){
	return fa[x]==x?x:getfa(fa[x]);
}
void marge(int x,int y){
	fa[getfa(y)]=getfa(x);
}

由于 Tarjan 是在遍历到目标点的时候得出答案并输出，那么如果你不输出,就需要使用一些东西来记录它（一般不用）。

关于记录

除非你之后需要 LCA 的结果再做一些操作，否则不需要记录，直接在 DFS 中输出即可。

我使用的是 STL 中的 Map 和 Pair，因为 LCA 是求两个点，Pair 正好可以满足一对数据。而 Map 的哈希机制可以实现 O(1) 查找。

Tarjan 求 LCA 做法

总体思想

遍历每一个结点并使用并查集记录父子关系。

Tarjan 是一种 DFS 的思想。我们需要从根结点去遍历这棵树。

当遍历到某一个结点(称之为 x) 时，你有以下几点需要做的。

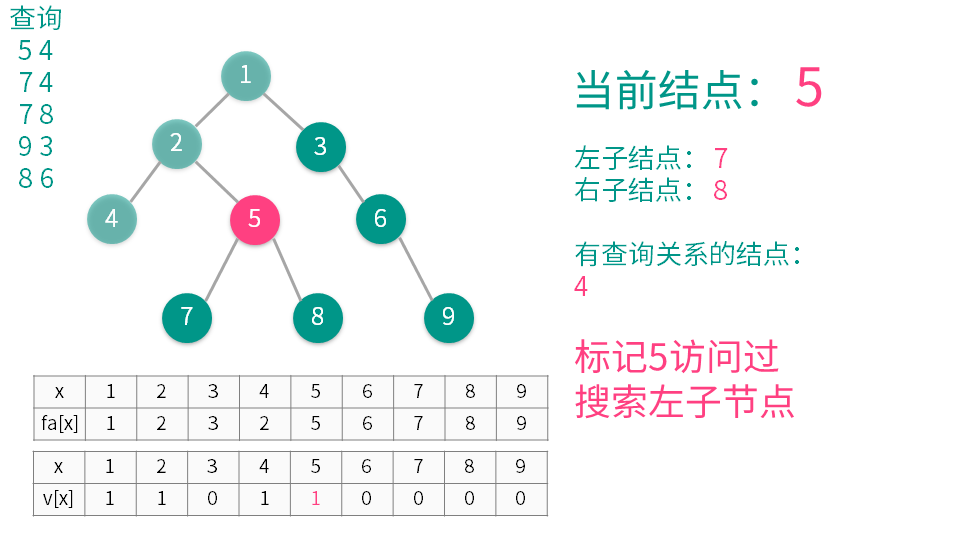
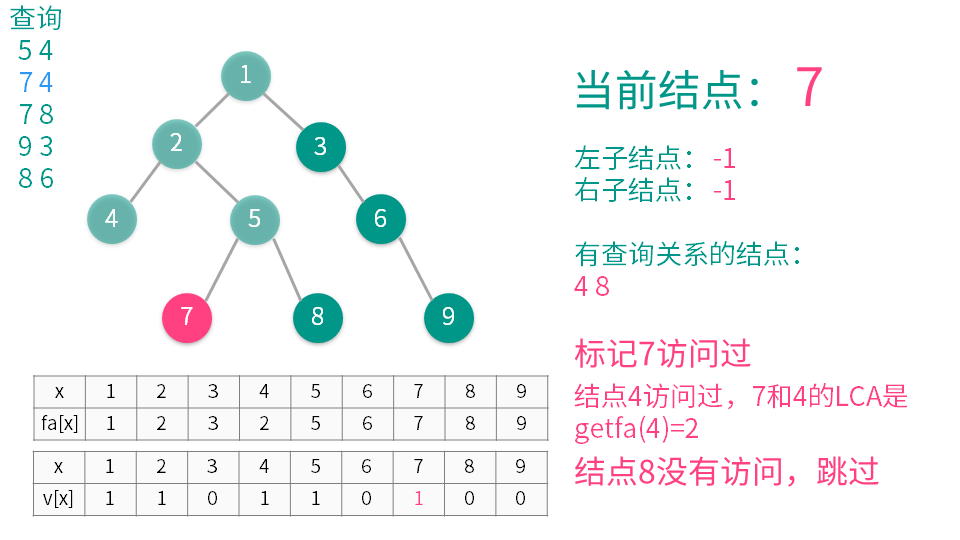
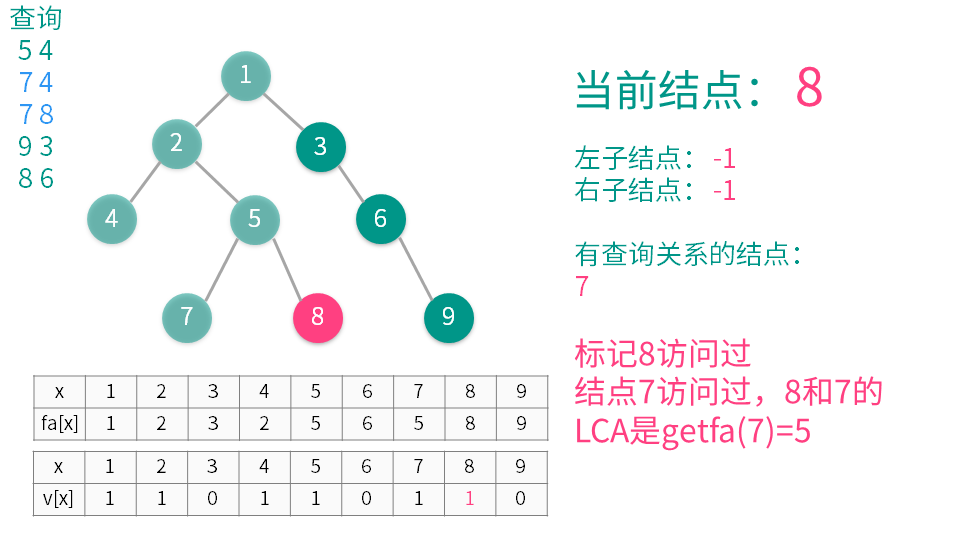
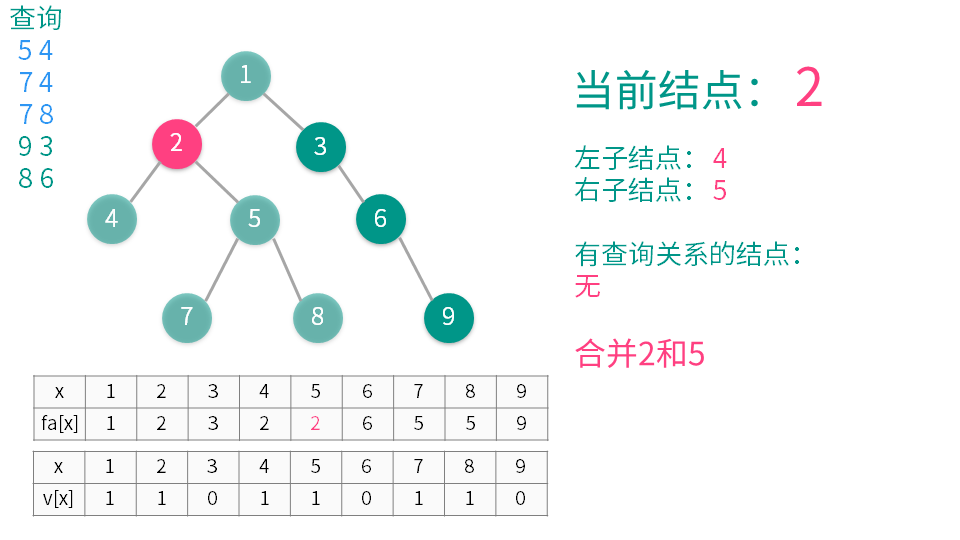
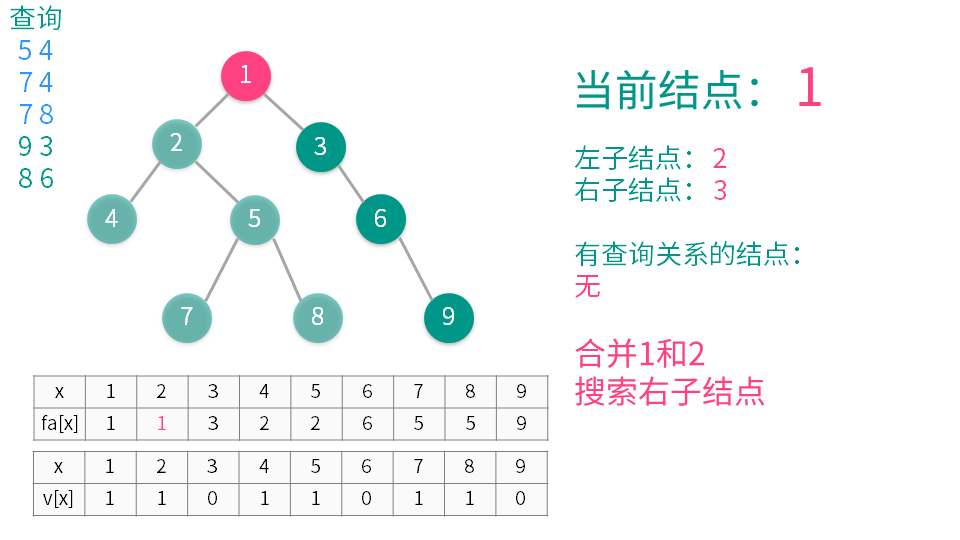
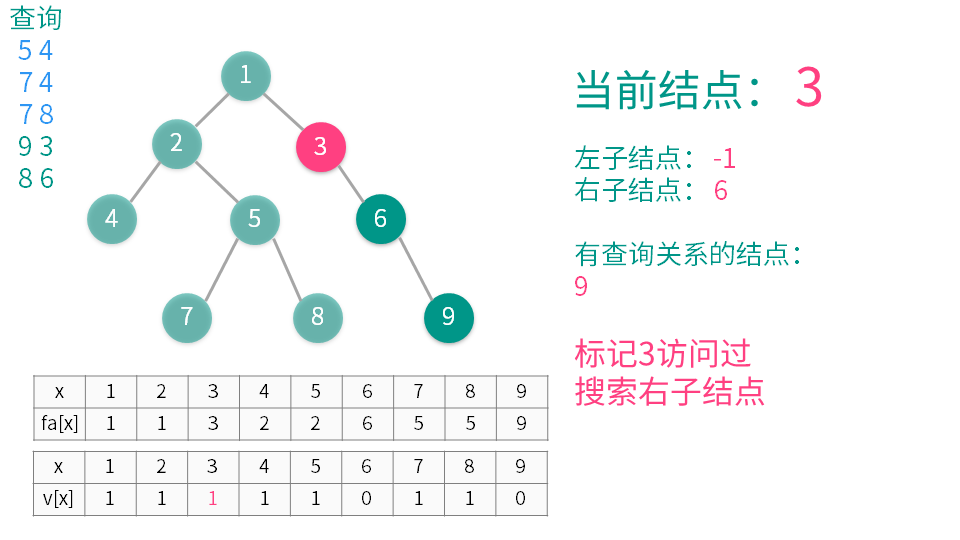
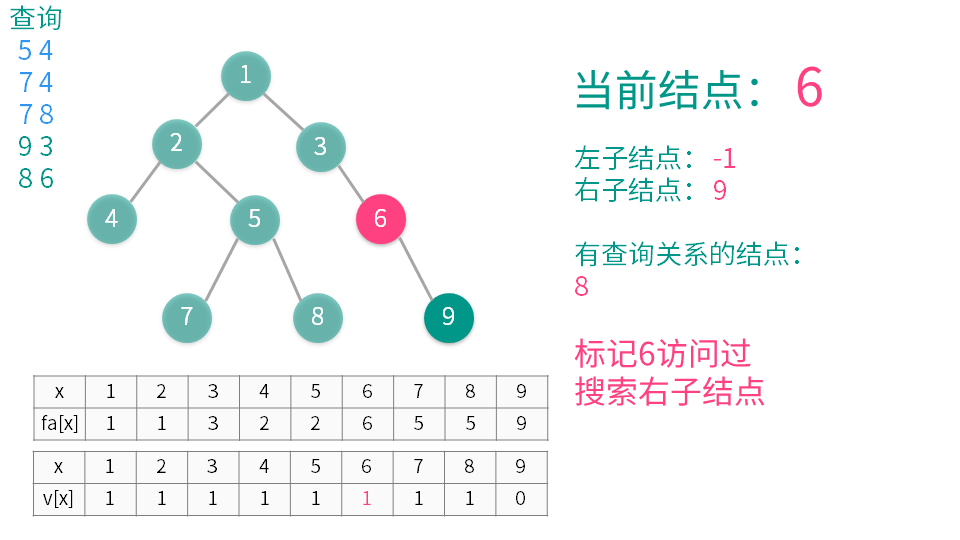
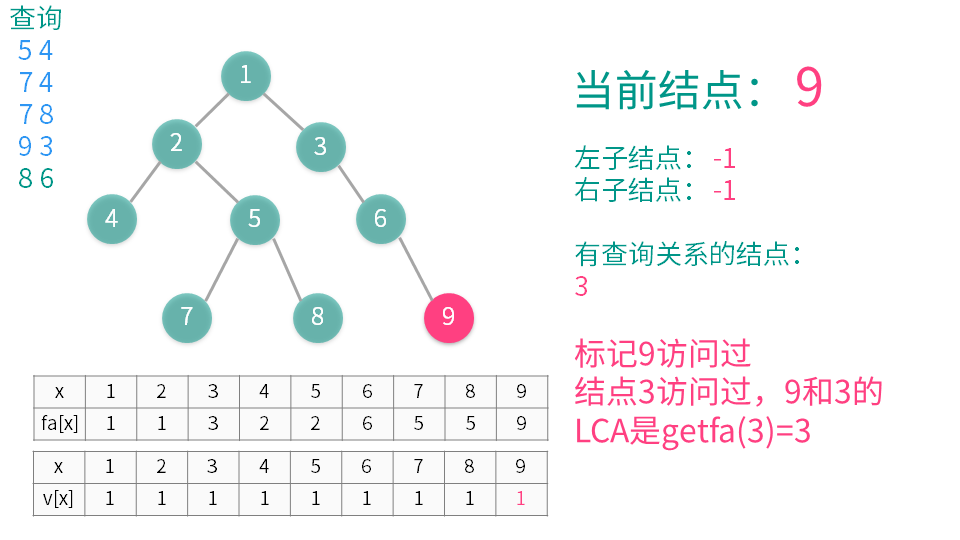
1将当前结点标记为已经访问。

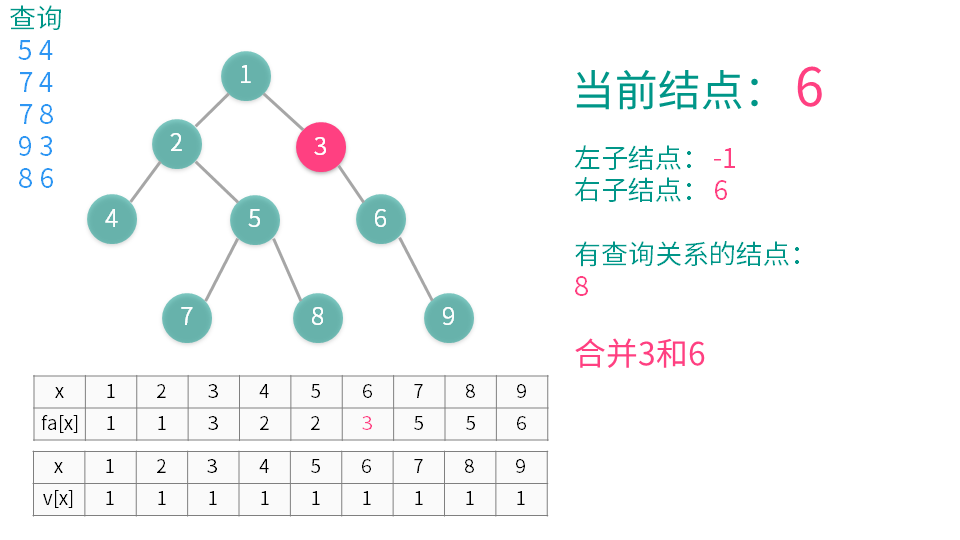
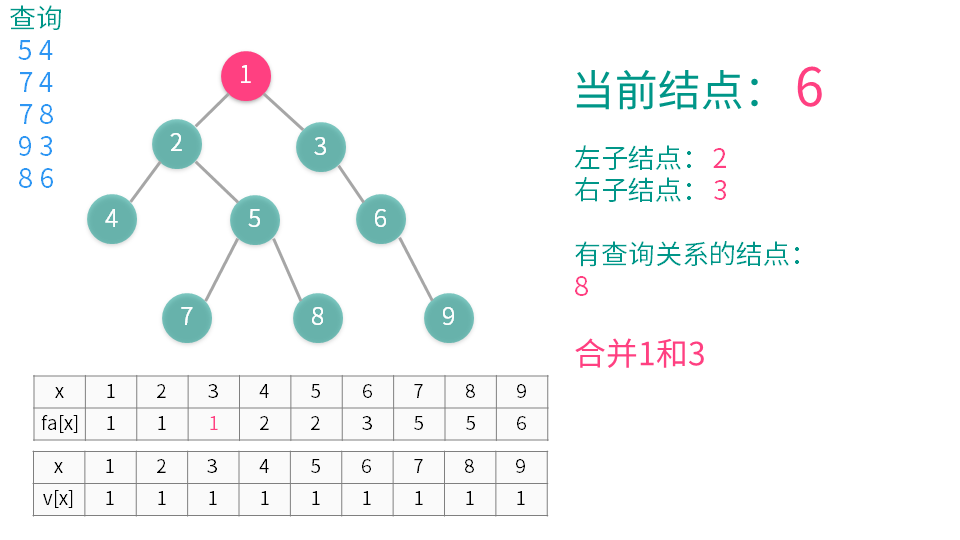
2递归遍历所有它的子节点(称之为 y)，并在递归执行完后用并查集合并 x 和 y。

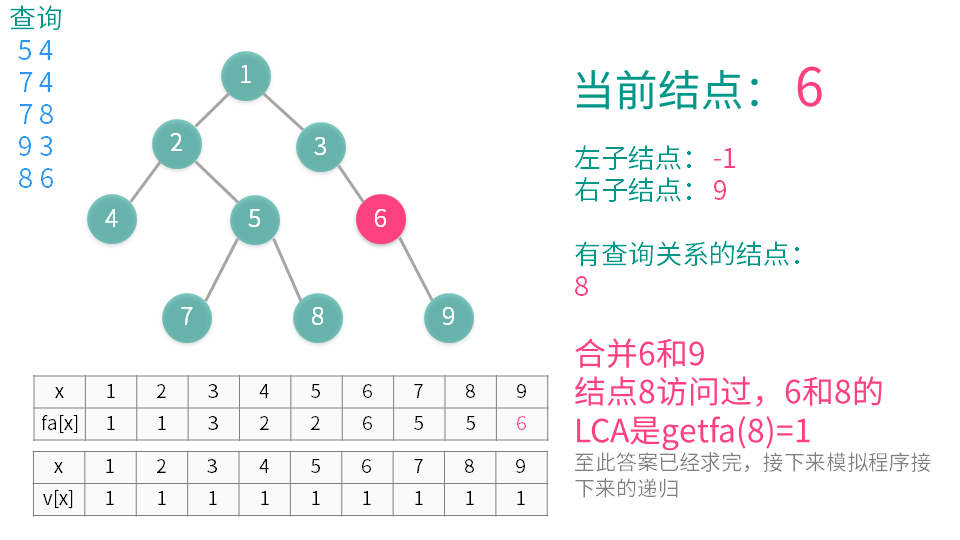
3遍历与当前节点有查询关系的结点(称之为 z)(即是需要查询 LCA 的另一些结点)，如果 z 已经访问，那么 x 与 z 的 LCA 就是 $getfa(z)$(这个是并查集中的查找函数)，输出或者记录下来就可以了。

这是伪代码

void tarjan(int x){
    //在本代码段中，s[i]为第i个子节点 , t[i]为第i个和当前节点有查询关系的结点。
    vis[x]=1;//标记已经访问，vis是记录是否已访问的数组
    for (i=1;i<=子节点数;i++){//枚举子节点 (递归并合并)
        tarjan(s[i]);
        marge(x,s[i]);//并查集合并
    }
    for (i=1;i<=有查询关系的结点数;i++){
        if (vis[t[i]]){
            cout<<x<<"和"<<t[i]<<"的LCA是"<<getfa(t[i])<<endl;//如果t[i]已经访问了输出(getfa是并查集查找函数)
        }
    }
}

核心代码就这么一点？对，就这么一点。

如果你还不理解，那么可以跳转到最后一章看图解演示。

一些重要的细节

为了接下来的讲解，下面我们明确一下读入方式，不同的读入方式可以自己变通一下。

第一行两个数 n 和 q，表示结点数和查询数。

接下来 n 行每行两个数，表示左子结点和右子结点编号，如没有则是 -1。

接下来 q 行每行两个数，表示查询的两个结点编号。

例如上图的树，读入为

9 5
2 3
4 5
-1 6
-1 -1
7 8
-1 9
-1 -1
-1 -1
-1 -1
5 4
7 4
7 8
9 3
8 6

如何存储查询关系

我在这里用的方法是二维数组。

int t[100000][10],top[100000];
//t[i][j]表示编号为i的结点，第j个和它有查询关系的点的编号
//top[i]表示编号为i的结点与它有查询关系的点的数量

　　

注意：需要双向存储关系。例如结点 2 和 3，不仅要更新t[2]，还要更新t[3]。

读入代码长这样：

for (int i=1;i<=q;i++){
	cin>>a[i]>>b[i];
	t[a[i]][++top[a[i]]]=b[i];
	t[b[i]][++top[b[i]]]=a[i];
}

当然如果你想要优化下空间那么把这个数组变成vector也是没问题的。

这就没了...

代码

直接输出的写法

#include<bits/stdc++.h>
using namespace std;
int n,k,q,v[100000];
map<pair<int,int>,int> ans;//存答案
int t[100000][10],top[100000];//存储查询关系
struct node{
	int l,r;
};
node s[100000];
/*并查集*/
int fa[100000];
void reset(){
	for (int i=1;i<=n;i++){
		fa[i]=i;
	}
}
int getfa(int x){
	return fa[x]==x?x:getfa(fa[x]);
}
void marge(int x,int y){
	fa[getfa(y)]=getfa(x);
}
/*------*/
void tarjan(int x){
	v[x]=1;//标记已访问
	node p=s[x];//获取当前结点结构体
	if (p.l!=-1){
		tarjan(p.l);
		marge(x,p.l);
	}
	if (p.r!=-1){
		tarjan(p.r);
		marge(x,p.r);
	}//分别对l和r结点进行操作
	for (int i=1;i<=top[x];i++){
		if (v[t[x][i]]){
			cout<<getfa(t[x][i])<<endl;
		}//输出
	}
}
int main(){
	cin>>n>>q;
	for (int i=1;i<=n;i++){
		cin>>s[i].l>>s[i].r;
	}
	for (int i=1;i<=q;i++){
		int a,b;
		cin>>a>>b;
        	t[a][++top[a]]=b;//存储查询关系
        	t[b][++top[b]]=a;
	}
	reset();//初始化并查集
	tarjan(1);//tarjan 求 LCA
}

先记录而不输出的写法

#include<bits/stdc++.h>
using namespace std;
int n,k,q,v[100000];
map<pair<int,int>,int> ans;//存答案
int t[100000][10],top[100000];//存储查询关系
int a[100000],b[100000];
struct node{
	int l,r;
};
node s[100000];
/*并查集*/
int fa[100000];
void reset(){
	for (int i=1;i<=n;i++){
		fa[i]=i;
	}
}
int getfa(int x){
	return fa[x]==x?x:getfa(fa[x]);
}
void marge(int x,int y){
	fa[getfa(y)]=getfa(x);
}
/*------*/
void tarjan(int x){
	v[x]=1;
	node p=s[x];
	if (p.l!=-1){
		tarjan(p.l);
		marge(x,p.l);
	}
	if (p.r!=-1){
		tarjan(p.r);
		marge(x,p.r);
	}
	for (int i=1;i<=top[x];i++){
		if (v[t[x][i]]){
			pair<int,int> tmp,tmp1;//用pair配合map来存储答案
			tmp=make_pair(x,t[x][i]);
			tmp1=make_pair(t[x][i],x);//两个pair的目的是例如3 2这种数据如果搜到3才有答案那么进时的顺序不止是(3,2)，还有(2,3)，方便输出结果时查询
			ans[tmp]=getfa(t[x][i]);
			ans[tmp1]=getfa(t[x][i]);
			cout<<"#"<<ans[tmp]<<endl;
		}
	}
}
int main(){
	cin>>n>>q;
	for (int i=1;i<=n;i++){
		cin>>s[i].l>>s[i].r;
	}
	for (int i=1;i<=q;i++){
		cin>>a[i]>>b[i];
		t[a[i]][++top[a[i]]]=b[i];
		t[b[i]][++top[b[i]]]=a[i];
	}
	reset();
	tarjan(1);
	for (int i=1;i<=q;i++){
		pair<int,int> tmp;
		tmp=make_pair(b[i],a[i]);
		cout<<a[i]<<"-"<<b[i]<<":"<<ans[tmp]<<endl;
	}
}

算法演示

 

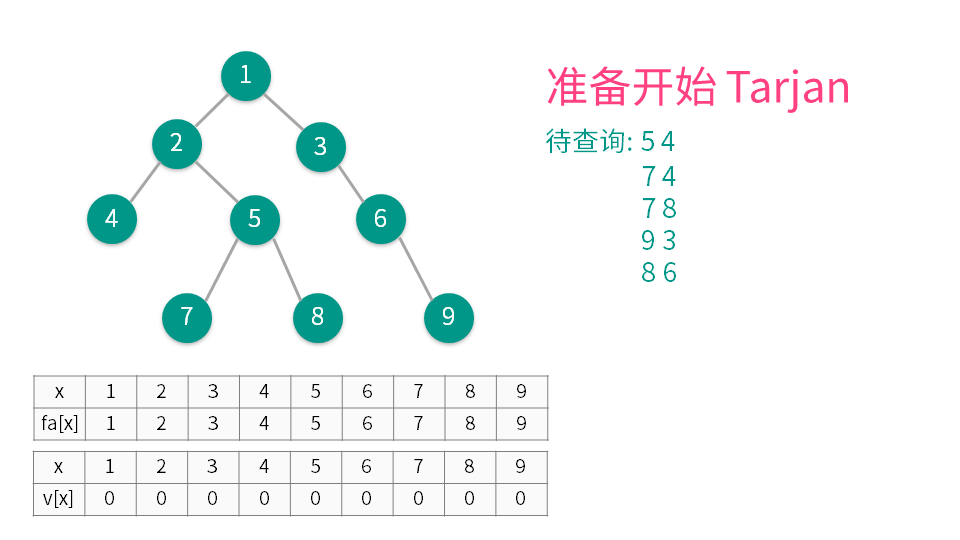
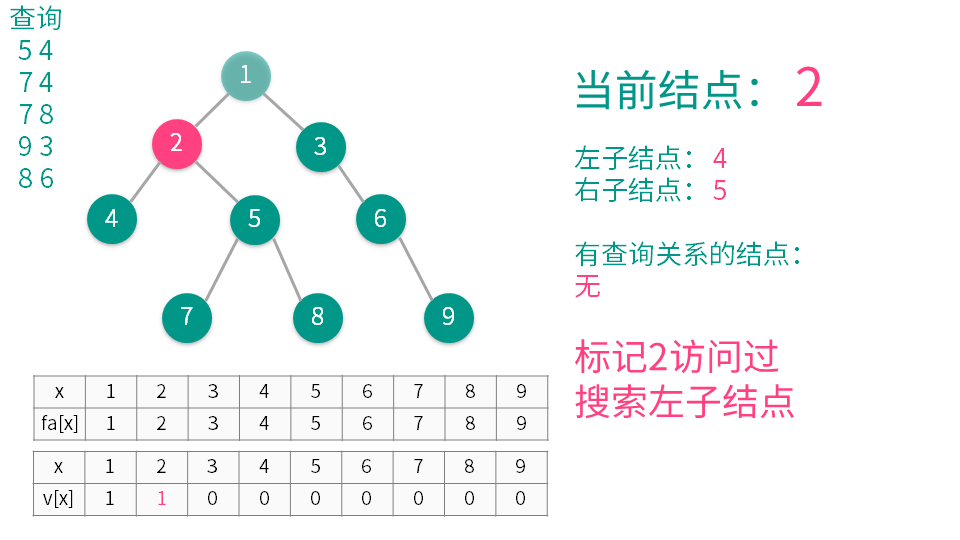
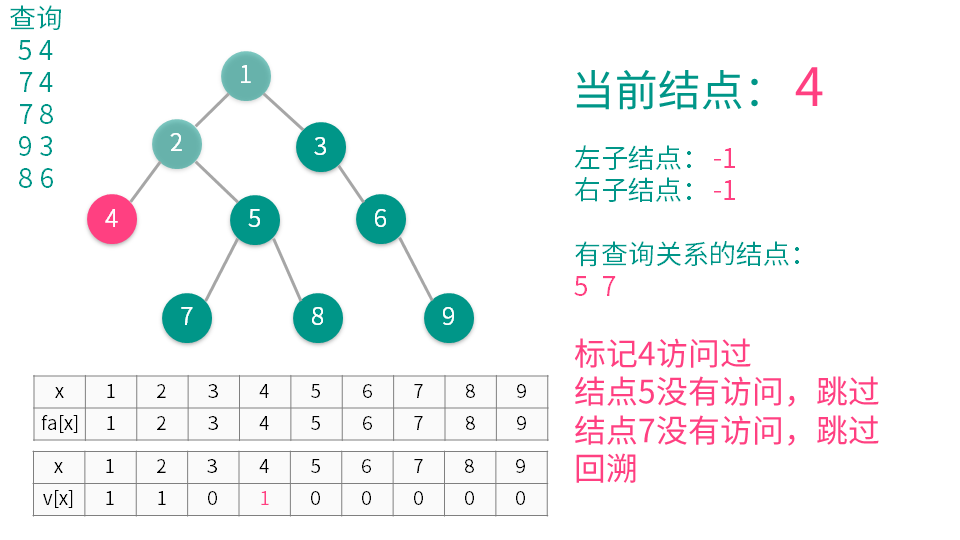
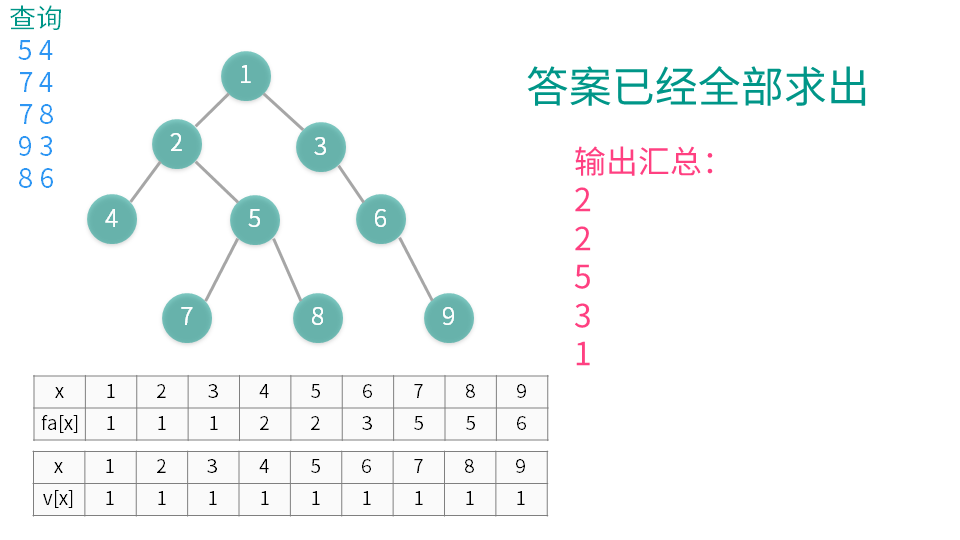
下一步 上一步