KMP算法（——模板习题与总结）

　　KMP算法是一种改进的模式匹配算法，相比于朴素的模式匹配算法效率更高。下面讲解KMP算法的基本思想与实现。

　　先来看一下朴素模式匹配算法的基本思想与实现。

　　朴素模式匹配算法的基本思想是匹配过程中如果该位置相等，继续匹配各自的下一位，直至匹配完成，或者出现一位不匹配，如果该位置不相等，主串的匹配位置返回上次开始匹配位置的下一位，副串的匹配位置再次从头开始。

实现程序如下：

　　主串s，副串t，如果存在，返回t在s中第一次出现的位置，否则返回-1。

 int Index(char *s,char *t){
     int ls=strlen(s),lt=strlen(t);
     int i=;//主串匹配位置
     int j=;//副串匹配位置
     while(i < ls && j < lt){
         if(s[i] == t[j]){
             i++;
             j++;
         }
         else{
             i=i-j+;
             j=;
         }
     }
     if(j >= lt)//副串匹配完成
         return i-j;
     else
         return -;
 }

　　可以设想，最糟糕的情况是每次的匹配的不成功均发生在了最后一位匹配，那么它的时间就主要浪费在了主串回溯的过程，比如00000001（7个0）和001，就有5次回溯是不必要的，它浪费的时间是随着匹配成功之间的0的个数增多而增多，自然就想到没有什么办法去解决这个问题呢？

　　下面就轮到KMP算法登场了。

　　为了解决每次主串匹配不成功尽可能的往右边滑的更远一点问题，自然想到充分利用现在已知的信息，这里借鉴《算法竞赛入门经典 训练指南》中的图解，具体体会一下KMP算法的精髓。

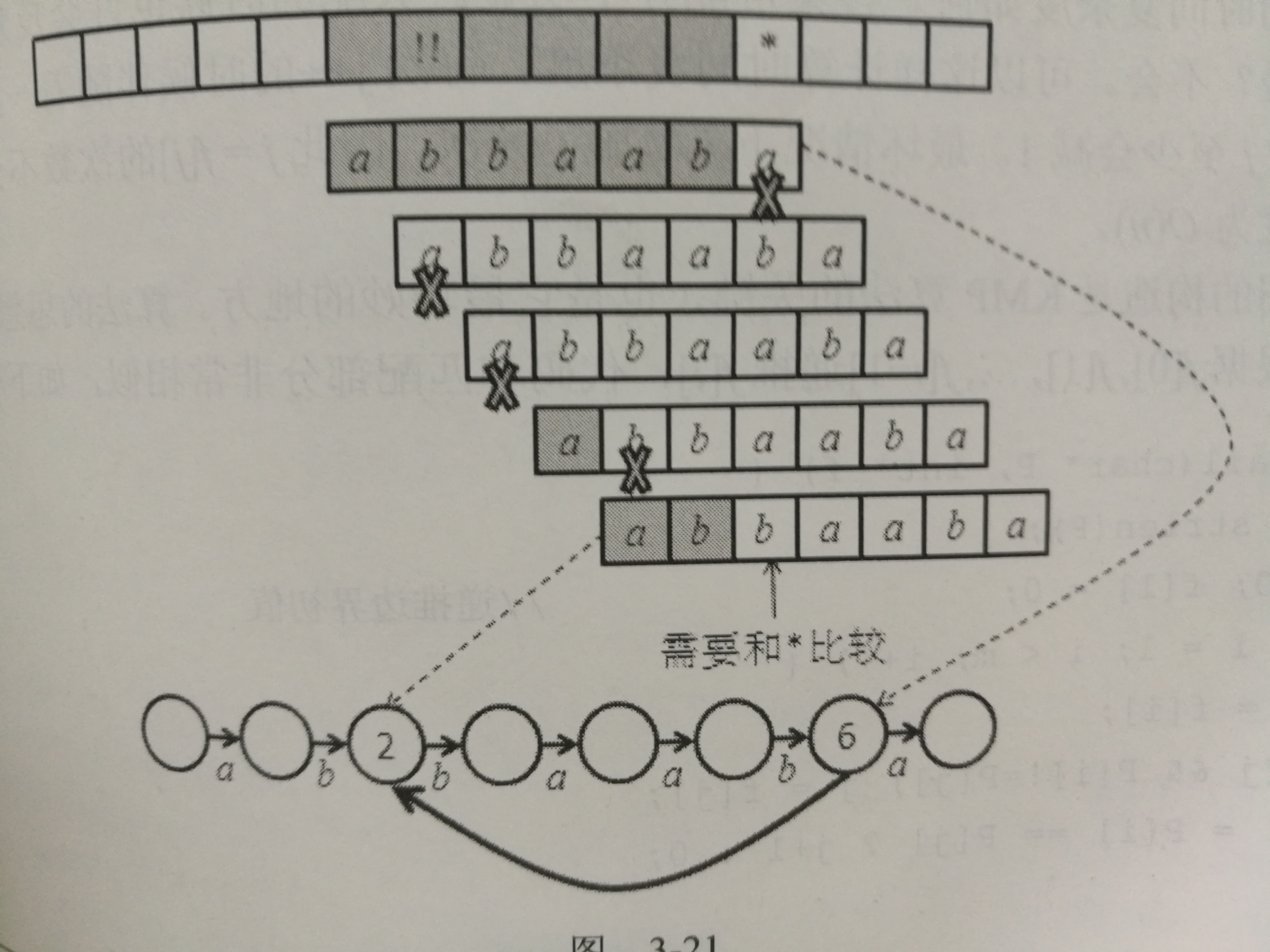
　　假如现在正在匹配主串中*位置和副串abbaaba的最后一个字符，发现二者不同（称为失配），这时，朴素算法的做法是将串的开头放在!!的位置上重新开始匹配，但KMP算法为了让副串尽可能的回溯少一点，就利用现在已知的全部副串的信息来构建一个发现失配后副串尽可能的往右滑的更远的状态转移图，例如根据之前的匹配，我们知道了主串中*之前的副串长度的字符串，因为到*的时候才失配，我们可以知道副串右移一位、右移两位甚至三位都是不行的，因为和自己匹配失败，但是右移四位的时候就可能和后面的匹配了。这个右移的比较过程实际上就是一个串的前缀和后缀匹配的过程，为了滑的更远，我们需要找到两者最大的相似度，我们发现当走到副串的最后一个位置发现不匹配时前面的串的前后缀最大相似度是2，也就是ab的长度，故图中可以看到当最后一个字符失配的时候下面的实体黑线指向了2，就完成了往右滑的尽可能远的任务。

　　那么怎么计算一个子串的前后缀的相似度呢？

　　我们用next[j]数组来表示j下次应该返回的位置,函数定义如下：

　　next[j]=   0,当j=0

　　　　　　max({k|0<k<=j,且p0...pk=p(j-k)...pj}，当此集合不为空

　　　　　　1，其他

算法实现如下：

　　副串t，用next数组存储结果。

 void get_next(char t[],int next[])
 {
     int l=strlen(t);
     int i=;//副串匹配位置
     int j=-;//next数组位置指针，初始化为-1，表示回溯边界
     next[]=-;//0表示长度为0的子串的前后缀相似度为-1，也表示回溯边界
     while(i < l){
         if(j == - || t[i] == t[j]){
             i++;
             j++;
             next[i]=j;
         }
         else
             j=next[j];
     }
 }

下面将制作好的next数组应用到KMP算法中。

代码如下：

 int Index_KMP(char *s,char *t){
     int ls=strlen(s),lt=strlen(t);
     int i=;//主串起始匹配位置
     int j=;//副串起始匹配位置
     int next[maxn]={};
     get_next(t,next);
     while(i < ls && j < lt){
         if(j == - || s[i] == t[j]){//增加j==-1表示回溯到了边界的情况
             i++;
             j++;
         }
         else{
             j=next[j];//j返回到合适的位置，而i不用改变
         }
     }
     if(j >= lt)//匹配完成
         return i-j;
     else
         return -;
 }

　　可以看到KMP算法相较朴素的模式匹配算法，多了制作next数组，多了一个判断条件，就成功的避免了主串不必要的回溯，节省了时间。下面给出几道练习题目，巩固知识。

　　1.简单的模板题HDU 1711 Number Sequence

　　https://www.cnblogs.com/wenzhixin/p/7345115.html

　　2.需要一点思维转换HDU 2203 亲和串

　　https://www.cnblogs.com/wenzhixin/p/7344076.html

　　3.加深印象HDU 3746 Cyclic Nacklace

　　https://www.cnblogs.com/wenzhixin/p/7345115.html

　　其他练习参考右侧分类中的KMP。