[CSP-S模拟测试]:电压机制（图论+树上差分）

题目描述

科学家在“无限神机”（$Infinity\ Machine$）找到一个奇怪的机制，这个机制有$N$个元件，有$M$条电线连接这些元件，所有元件都是连通的。两个元件之间可能有多条电线连接。
科学家对这些元件可以任意地设置为“高电压”和“低电压”两种模式，如果一条电线的一端为高电压，另一端为低电压，这条电线就会产生电流。
为了安全的研究“无限神机”，科学家需要找到一条电线，将它的两端设为相同的电压，并且除选择的这条电线外，其它所有电线都有电流（否则就没有研究的价值了）。
有多少条电线满足这样的条件？

---

输入格式

输入的第一行包含两个正整数$n,m$，表示元件数和电线数。
接下来$m$行，每行两个整数$u,v$，表示元件$u$和元件$v$有一条电线连接

---

输出格式

输出一个整数，表示有多少条电线满足条件

---

样例

样例输入1：

4 5
1 2
1 3
1 4
2 4
3 4

样例输出1：

1

样例输入2：

4 4
1 2
2 3
3 2
4 3

样例输出2：

2

---

数据范围与提示

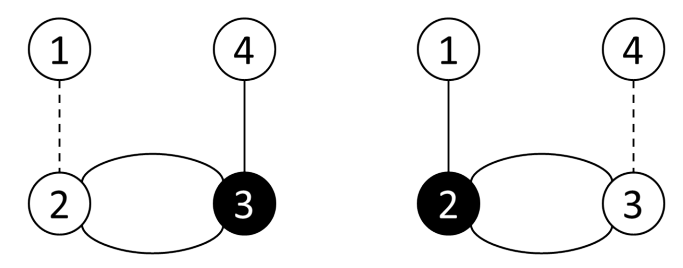
样例$1$解释：

如图，只有电线$(1,4)$满足

样例$2$解释：

电线$(1,2)$和$(3,4)$满足要求

数据范围：

对于$10/%$的数据，满足$n\leqslant 1,000,m\leqslant 2,000$
对于另外$10/%$的数据，满足$m=n$
对于另外$35/%$的数据，满足$m\leqslant n+100$
对于$100/%$的数据，满足$2\leqslant n\leqslant 100,000,1\leqslant m\leqslant 200,000$

---

题解

再一次被语文打倒（可能是我语文太菜了叭～）……

先来解释一下题意，在样例$2$中$2$和$3$之间的边之所以不能设成相同的电压，是因为之后剩下那条边两端的电压就相同了，也就没有电流了。

为方便，不妨将一条电线两端电压设成相同成为“删”掉这条边。

话个图我们便会发现，偶环中的都不能删，如下图中无论删掉哪条边，对面的边两端电压都会相同。

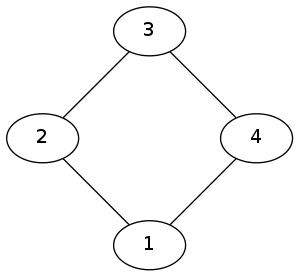
但是，不在偶环里的就一定能删吗？

看下面这一张图$\downarrow$

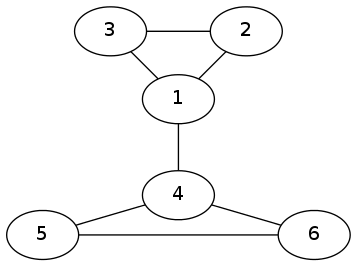
可以发现，$(2,3)$和$(5,6)$互相牵制，都不能删。

于是我们还可以推得，一条边必须能被所有奇环包含并且不被任何偶环包含才能被删。

那么怎么求呢？

其实如果我说利用树上差分思想就不那么难了，先建一棵$DFS$树，剩下的边全部为反祖边，判断环是奇是偶然后分别用两个数组记录即可（设这条边从$u$到$v$，$v$是祖先，在$u$处$--$并在$v$处$++$即可）。

注意数据并没有保证联通！！！

时间复杂度：$\Theta(n+m)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;bool dead;}e[400002];
int head[100001],cnt=1;
int n,m;
int odd[100001],eve[100001],cut[400002],depth[100001],in[100001];
bool vis[100001];
int ans;
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void dfs(int x)
{
	vis[x]=1;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(cut[i])continue;
		cut[i]=cut[i^1]=1;
		if(vis[e[i].to])
		{
			if((depth[x]-depth[e[i].to])&1){eve[e[i].to]--;eve[x]++;}
			else{odd[e[i].to]--;odd[x]++;odd[0]++;}
		}
		else
		{
			depth[e[i].to]=depth[x]+1;
			in[e[i].to]=i;
			dfs(e[i].to);
		}
	}
}
void dfs(int x,int f)
{
	for(int i=head[x];i;i=e[i].nxt)
		if(in[e[i].to]==i)
		{
			dfs(e[i].to,x);
			odd[x]+=odd[e[i].to];
			eve[x]+=eve[e[i].to];
		}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);add(v,u);
	}
	for(int i=1;i<=n;i++)if(!vis[i])dfs(i);
	if(odd[0]==1)ans=1;
	for(int i=1;i<=n;i++)if(!in[i])dfs(i,0);
	for(int i=1;i<=n;i++)
		if(in[i]&&odd[i]==odd[0]&&!eve[i])ans++;
	printf("%d",ans);
	return 0;
}

---

rp++