【BZOJ1521】Est（单调队列优化DP）

题意：From https://www.cnblogs.com/CXCXCXC/p/4725249.html

思路：本身就两维状态了，把问题关键s[i][j]写成二维比一维好写多了

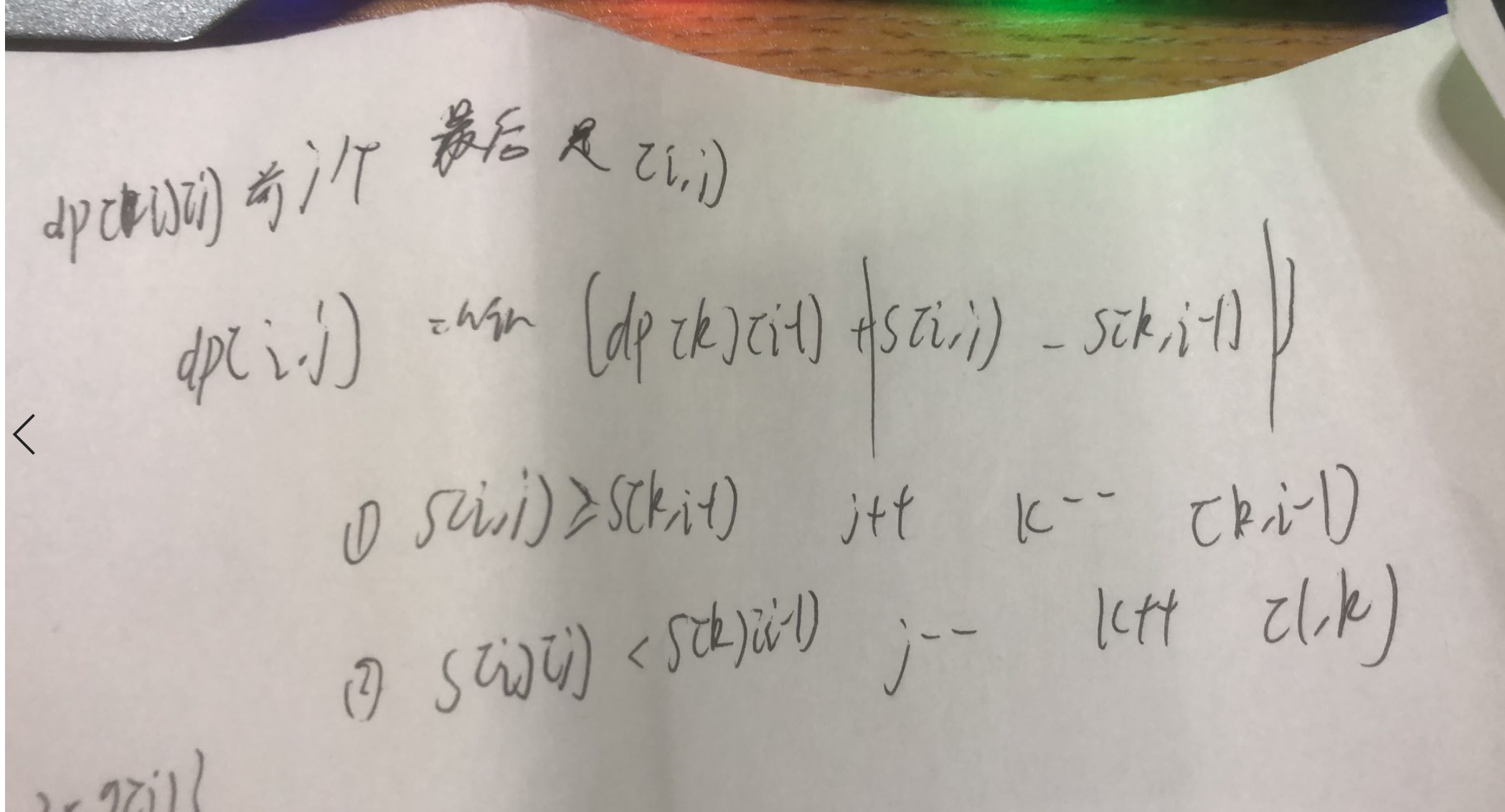
 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef long double ld;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 typedef vector<PII> VII;
 //typedef pair<ll,ll>P;
 #define N  2010
 #define M  200010
 #define INF 1e9
 #define fi first
 #define se second
 #define MP make_pair
 #define pb push_back
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=1e9+,inv2=(MOD+)/;
       double eps=1e-;
       int dx[]={-,,,};
       int dy[]={,,-,};

       int dp[N][N],s[N][N],a[N];

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     int m=read(),n=read();
     rep(i,,n) a[i]=read();
     rep(i,,n)
      rep(j,i,n) s[i][j]=s[i][j-]+a[j]+(j!=i);
     rep(i,,n+)
      rep(j,,n+) dp[i][j]=INF;
     rep(i,,n)
      if(s[][i]<=m) dp[][i]=;
     rep(i,,n)
     {
         int k=i,mn=INF;
         rep(j,i,n)
          if(s[i][j]<=m)
          {
              while(k>&&s[k-][i-]<=s[i][j])
              {
                  k--;
                  mn=min(mn,dp[k][i-]-s[k][i-]);
              }
              dp[i][j]=mn+s[i][j];
          }
          k=,mn=INF;
          per(j,n,)
           if(s[i][j]<=m)
           {
               while(k<=i&&s[i][j]<=s[k][i-])
               {
                   mn=min(mn,dp[k][i-]+s[k][i-]);
                   k++;
               }
               dp[i][j]=min(dp[i][j],mn-s[i][j]);
           }
     }
     int ans=INF;
     rep(i,,n) ans=min(ans,dp[i][n]);
     printf("%d\n",ans);
     return ;
 }