2019牛客暑期多校训练营（第三场）H Magic Line

原题链接：H  Magic Line

题意简述：

　　给定n个点，要求画一条直线将n个点分成均有n / 2个点的两部分，不能有点在线上；

解题思路：

　　首先，先将所有的点进行以x为第一关键字，y为第二关键字进行排序，接着：

1. 如果a[n / 2 - 1] < a[n / 2]，那么则可以以(a[n / 2 - 1].x，INF)，(a[n / 2].x，- INF)这两点画一条符合题意的直线【但是我试了(a[n / 2 - 1].x，a[n/2-1].y + INF) (a[n / 2].x，a[n/2].y - INF)也是可以的】
2. 如果a[n / 2 - 1] == a[n / 2]，那么则可以根据(a[n / 2].x - 1，a[n / 2].y + INF)，(a[n / 2 - 1].x + 1，a[n / 2 - 1].y - INF)这两题画一条符合题意的直线；

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　第一种情况

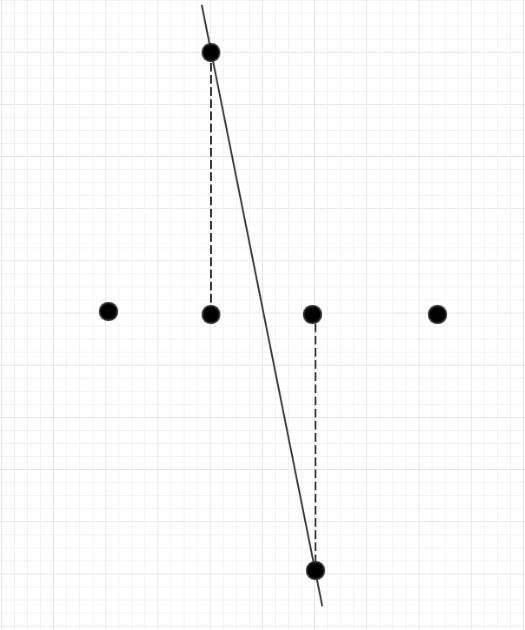
对于第二种情况，我们首先根据a1(a[n / 2].x - 1，a[n / 2].y + INF)这点做出关于(a[n / 2].x，a[n / 2].y)的对称点a2(a[n / 2].x + 1，a[n / 2].y - INF)，由于a[n / 2].x == a[n / 2 - 1].x ，并且a[n / 2].y > a[n / 2 - 1].y，那么我们可以将(a[n / 2 - 1].x，a[n / 2 - 1].y - INF)看作是a2点向下移了一点（记为a2'），那么此时的a2'与a1这两点确定的直线必定符合题意；

代码如下：(参考自咖啡鸡)

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> pi;
pi a[];
int n,T;
const int E=;

int main(){
    cin >> T;
    while (T--){
        cin >> n;
        for (int i = ; i < n; i++) cin >> a[i].x >> a[i].y;
        sort(a, a + n);
        if (a[n/ - ].x<a[n/].x)    printf("%d %d %d %d\n", a[n/-].x, a[n/-].y + E, a[n/].x, a[n/].y - E);
        else    printf("%d %d %d %d\n", a[n/].x - , a[n/].y + E, a[n/].x + , a[n/-].y - E);
    }
}

Magic Line