BUUCTF平台：RSA

RSA

import gmpy2

def Decrypt(c,e,p,q):
	L=(p-1)*(q-1)
	d=gmpy2.invert(e,L)
	n=p*q
	m=gmpy2.powmod(c,d,n)
	flag=str(d)
	print("flag{"+flag+"}")

if __name__ == '__main__':
	p=473398607161
	q=4511491
	e=17
	c=55
	Decrypt(c,e,p,q)

rsarsa

import gmpy2

def Decrypt(c,e,p,q):
	L=(p-1)*(q-1)
	d=gmpy2.invert(e,L)
	n=p*q
	m=gmpy2.powmod(c,d,n)
	flag=str(m)
	print("flag{"+flag+"}")

if __name__ == '__main__':
	p =  9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
	q =  11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
	e =  65537
	c =  83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

	Decrypt(c,e,p,q)

RSA1

题目中的dp,dq，开始并不知道这是个啥，看过WriteUp后才得知，但现在也还没有明白最后怎么推出来的，可以参考下面：

https://www.cnblogs.com/P201521440001/p/11415504.html#rsa%E7%B3%BB%E5%88%97

https://beiyuouo.github.io/blog/ctf-buuctf/

import gmpy2
import binascii
def decrypt(dp,dq,p,q,c):
	InvQ = gmpy2.invert(q,p)
	mp = pow(c,dp,p)
	mq = pow(c,dq,q)
	m=(((mp-mq)*InvQ)%p)*q+mq
	temp_flag=binascii.unhexlify(hex(m)[2:])
	flag='flag'+temp_flag[6:]
	print(flag)
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

decrypt(dp,dq,p,q,c)

RSA3

共模攻击，前面的文章中也讲到过了，这里就不再去赘述了，直接上师傅的代码

import gmpy2 as gp

def exgcd(a, b):
    if b==0:
        return 1, 0, a
    x2, y2, r = exgcd(b, a%b)
    x1 = y2
    y1 = x2-(a//b)*y2
    return x1, y1, r

c1=gp.mpz(22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361)
n=gp.mpz(22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801)
e1=gp.mpz(11187289)
c2=gp.mpz(18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397)
e2=gp.mpz(9647291)

r1, r2, t = exgcd(e1, e2)
m = gp.powmod(c1, r1, n) * gp.powmod(c2, r2, n) % n
# print(m)
# print(hex(m)[2:])
print(bytes.fromhex(str(hex(m)[2:])))

RSA2

这次告知了e,n,dp,c

RSA

解压出来flag.enc和pub.key

openssl rsa -pubin -text -modulus -in warmup -in pub.key

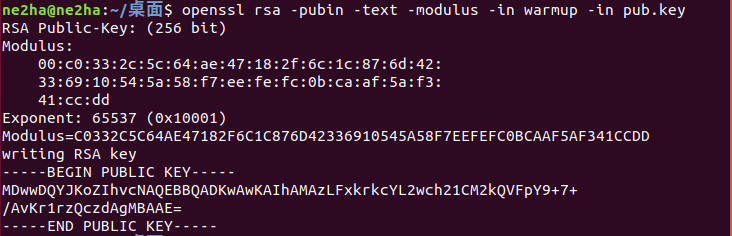
得到：
e=65537
n=0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
=86934482296048119190666062003494800588905656017203025617216654058378322103517
分解n得到：
p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463

通过rsatool工具生成私钥文件：

https://github.com/ius/rsatool

python2 rsatool.py -o private.pem -e 65537 -p 285960468890451637935629440372639283459 -q 304008741604601924494328155975272418463

通过openssl得到flag:

openssl rsautl -decrypt -in flag.enc -inkey private.pem

rsa2

RSAROOL

Dangerous RSA

RSA5

Same Mod

和RSA3一样的共模攻击

import gmpy2 as gp

def exgcd(a, b):
    if b==0:
        return 1, 0, a
    x2, y2, r = exgcd(b, a%b)
    x1 = y2
    y1 = x2-(a//b)*y2
    return x1, y1, r

def get_flag(string):
	flag=''
	i=0
	j=1
	while i < len(string):
		if int(string[i:i+j]) >= 33 and int(string[i:i+j]) <=126:
			flag+=chr(int(string[i:i+j]))
			i=i+j
			j=1
		else:
			j+=1
	print(flag)

if __name__ == '__main__':

	e1=773
	e2=839
	n=6266565720726907265997241358331585417095726146341989755538017122981360742813498401533594757088796536341941659691259323065631249
	message1=3453520592723443935451151545245025864232388871721682326408915024349804062041976702364728660682912396903968193981131553111537349
	message2=5672818026816293344070119332536629619457163570036305296869053532293105379690793386019065754465292867769521736414170803238309535
	r1, r2, t = exgcd(e1, e2)
	m = gp.powmod(message1, r1, n) * gp.powmod(message2, r2, n) % n
	get_flag(str(m))

RSA & what

RSA4