ajax实现异步请求模态登陆

ajax实现模态登陆

j2ee课程项目实现

  Ajax 即“Asynchronous Javascript And XML”（异步 JavaScript 和 XML），是指一种创建交互式网页应用的网页开发技术。

  Ajax = 异步 JavaScript 和 XML（标准通用标记语言的子集）。

---

使用场景

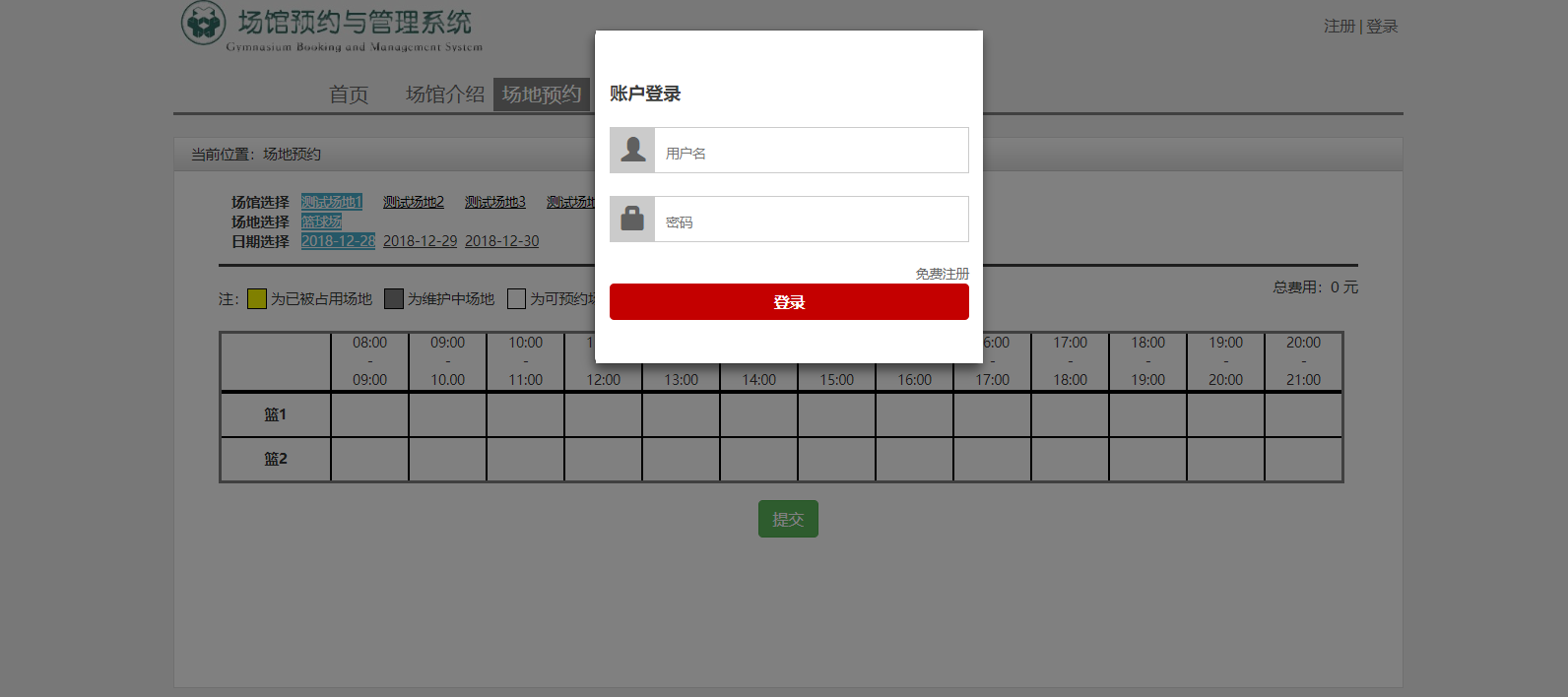
  通常，前台分为无需登录界面和需要登陆界面，以场地预约与管理系统为例，未登陆时场地的情况应当也是可见的，但是预约功能显然是不可使用的。所以在，未登录时点击预约应当弹出模态登陆的登陆框。如下图：

具体实现代码：

$(function () {
        //核对是否登陆
        $(".空闲").click(function(){

            var page = "forecheckLogin";
            var flag = 1;
            $.get(
                page,
                function(result){
                    if("success"==result) {
                        flag = 0;
                    } else {
                        $("#loginModal").modal('show');
                    }
                }
            );
            if (flag == 1) {
                this.style.backgroundColor = "white";
                document.getElementById("total").innerText = "0";
            }

            return true;
        });
        //模态登陆核对账号密码
        $("button.loginSubmitButton").click(function(){
            var name = $("#name").val();
            var password = $("#password").val();
            if(0==name.length||0==password.length){
                $("span.errorMessage").html("*请输入账号密码");
                $("div.loginErrorMessageDiv").show();
                return false;
            }
            var page = "foreloginAjax";
            $.get(
                page,
                {"name":name,"password":password},
                function(result){
                    if("success"==result){
                        location.reload();
                    }
                    else{
                        $("span.errorMessage").html("*账号密码错误");
                        $("div.loginErrorMessageDiv").show();
                    }
                }
            );
            return true;
        });
    })

<!--html部分-->
<div class="modal " id="loginModal" tabindex="-1" role="dialog" >
    <div class="modal-dialog loginDivInProductPageModalDiv">
        <div class="modal-content">
            <div class="loginDivInProductPage">

                <div class="alert" style="padding: 5px">
                    <span class="errorMessage" style="color: red;"></span>
                </div>

                <div class="login_acount_text">账户登录</div>
                <div class="loginInput " >
                            <span class="loginInputIcon ">
                                <span class=" glyphicon glyphicon-user"></span>
                            </span>
                    <input id="name" name="name"  type="text" placeholder="用户名">
                </div>

                <div class="loginInput " >
                            <span class="loginInputIcon ">
                                <span class=" glyphicon glyphicon-lock"></span>
                            </span>
                    <input id="password" name="password"  type="password" placeholder="密码" type="text">
                </div>
                <div>
                    <a href="register.jsp" class="pull-right">免费注册</a>
                </div>
                <div style="margin-top:20px">
                    <button class="btn btn-block redButton loginSubmitButton" type="submit">登录</button>
                </div>
            </div>
        </div>
    </div>
</div>