题解 P2763 【试题库问题】

这题可以用网络流，但我用的是匈牙利算法

---

进入正题

• 设第个类型需要个.将每个类型拆成个点，用一个边集数组记录它拆成的点。
• 第个试题有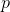个类型，分别将与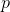拆成的点连边，这样便构成了一个二分图。
• 使用匈牙利算法计算最大匹配，若最大匹配小于的总数，则无解。
• 输出时使用优先队列。

OK了！！！

code：

---

• 拆点：

int main()
{
    for (int i=1;i<=k;i++)
    {
        need[i]=read();
        for (int j=1;j<=need[i];j++)Addedge(0,i,++cnt);
    }
}

---

• 将试题与类型连边：

void dot(int u,int v)
{
    for (int k=head[v];k>0;k=set[k].nx)
        Addedge(u,set[k].v);
    return ;
}

int main()
{
    int p;
    for (int i=1;i<=n;i++)
    {
        p=read();
        for (int j=1;j<=p;j++)dot(i,read());
    }
}

---

• 匈牙利算法：

bool dfs(int u)
{
    int v;
    for (int k=head[1][u];k>0;k=set[1][k].nx)
    {
        v=set[1][k].v;
        if (!vis[v])
        {
            vis[v]=true;
            if ((match[v]==-1)||dfs(match[v]))
            {
                match[v]=u;return true;
            }
        }
    }
    return false;
}

---

• 输出：

priority_queue<int,vector<int>,greater<int> > Q;
int main()
{
    for (int i=1;i<=k;i++)
    {
        printf("%d: ",i);
        for (int j=head[0][i];j>0;j=set[0][j].nx)Q.push(match[set[0][j].v]);
        while (!Q.empty()){printf("%d ",Q.top());Q.pop();}
        printf("\n");
    }
}

---

• 总代码：

#include <functional>
#include <cstdio>
#include <bitset>
#include <queue>
using namespace std;

int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0' || c>'9'){if (c=='-')f=-1;c=getchar();}
    while (c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48;c=getchar();}
    return x*f;
}

const int MAXK=25;
const int MAXN=1010;
int n,k,cnt;

struct edge
{
    int v,nx;
}set[2][MAXN*MAXN];
int id[2];
int head[2][MAXN];
int need[MAXK],match[MAXN*MAXN];
bitset<MAXN> vis;
priority_queue<int,vector<int>,greater<int> > Q;

inline void Addedge(int loca,int u,int v)
{
    id[loca]++;set[loca][id[loca]].v=v;set[loca][id[loca]].nx=head[loca][u];
    head[loca][u]=id[loca];
}

inline void dot(int u,int v)
{
    for (int k=head[0][v];k>0;k=set[0][k].nx)
        Addedge(1,u,set[0][k].v);
    return ;
}

inline bool dfs(int u)
{
    int v;
    for (int k=head[1][u];k>0;k=set[1][k].nx)
    {
        v=set[1][k].v;
        if (!vis[v])
        {
            vis[v]=true;
            if ((match[v]==-1)||dfs(match[v]))
            {
                match[v]=u;return true;
            }
        }
    }
    return false;
}

int main()
{
    k=read();n=read();
    for (int i=1;i<=k;i++)
    {
        need[i]=read();
        for (int j=1;j<=need[i];j++)Addedge(0,i,++cnt);
    }
    int p;
    for (int i=1;i<=n;i++)
    {
        p=read();
        for (int j=1;j<=p;j++)dot(i,read());
    }
    int ans=0;
    for (int i=1;i<=cnt;i++)match[i]=-1;
    for (int i=1;i<=n;i++)
    {
        vis.reset();
        if (dfs(i))ans++;
    }
    if (ans<cnt)puts("No Solution!");
    else
    {
        for (int i=1;i<=k;i++)
        {
            printf("%d: ",i);
            for (int j=head[0][i];j>0;j=set[0][j].nx)Q.push(match[set[0][j].v]);
            while (!Q.empty()){printf("%d ",Q.top());Q.pop();}
            printf("\n");
        }
    }
    return 0;
}
//丑代码

点赞吧