TopCoder SRM 559 Div 1 - Problem 900 CircusTents

传送门：https://284914869.github.io/AEoj/559.html

题目简述：

n个实心圆，两两没有交集，在第一个圆上找一个点，使得它到另外一个圆上某个点的最短距离的最小值尽量大，两个点之间的最短距离是指连接两个点且中途不进入任何一个实心圆内部的路径的长度的最小值。

二分答案：

很显然，这题跟二分答案有关。

思路：

我们先考虑，如果第一个圆上的点确定了下来，它到别的所有的圆的距离的最小值。

The First Case:

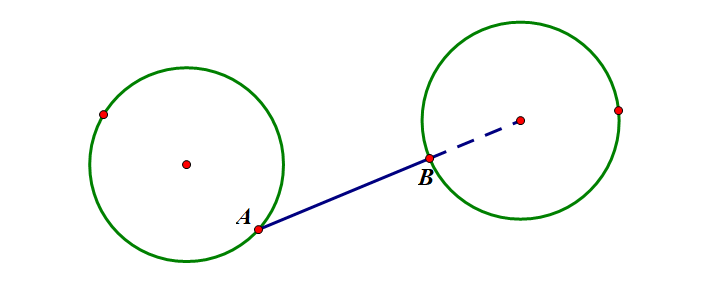
The Second Case:

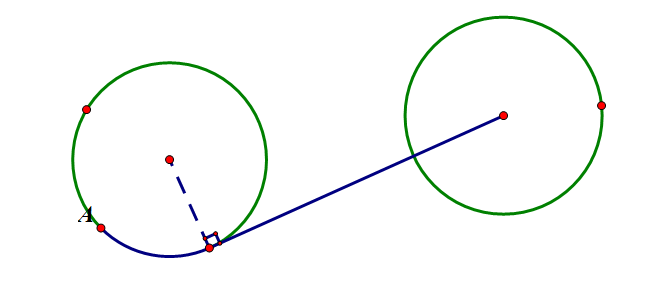
图中蓝色线是最短的路径。

当然还有第三种情况，就是路径过程中与别的圆相交了。不过这样肯定不是所有的路中最短的，所以可以忽略这种情况。

那么接下来考虑二分答案。

对于当前二分到的mid，

检查最终答案是否>=mid。

即是否存在最短路径都>=mid的点。

那么一个很简单的思路就出来了，对于每个圆，起点到它的最短路>=mid，可以确定起点一定不在圆上的某条弧上。

同样分两种情况，求出所有的起点位置限制。最后对这些位置限制（弧）排个序，判断合不合法即可。

题外话：

为了图方便，打算用余弦定理求位置限制，结果把公式背错了，对着样例调试了好久