AtCoder Beginner Contest 071 D - Coloring Dominoes

Problem Statement

We have a board with a 2×N grid. Snuke covered the board with N dominoes without overlaps. Here, a domino can cover a 1×2 or 2×1 square.

Then, Snuke decided to paint these dominoes using three colors: red, cyan and green. Two dominoes that are adjacent by side should be painted by different colors. Here, it is not always necessary to use all three colors.

Find the number of such ways to paint the dominoes, modulo 1000000007.

The arrangement of the dominoes is given to you as two strings S1 and S2 in the following manner:

• Each domino is represented by a different English letter (lowercase or uppercase).
• The j-th character in Si represents the domino that occupies the square at the i-th row from the top and j-th column from the left.

Constraints

• 1≤N≤52
• |S1|=|S2|=N
• S1 and S2 consist of lowercase and uppercase English letters.
• S1 and S2 represent a valid arrangement of dominoes.

---

Input

Input is given from Standard Input in the following format:

N
S1
S2

Output

Print the number of such ways to paint the dominoes, modulo 1000000007.

---

Sample Input 1

Copy

3
aab
ccb

Sample Output 1

Copy

6

There are six ways as shown below:

---

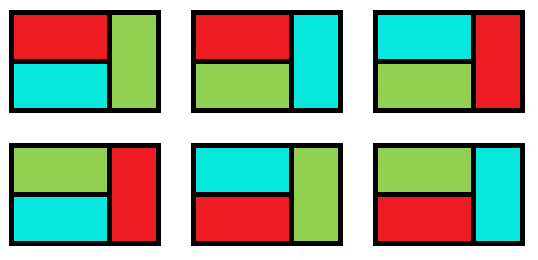
Sample Input 2

Copy

1
Z
Z

Sample Output 2

Copy

3

Note that it is not always necessary to use all the colors.

---

Sample Input 3

Copy

52
RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn
RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn

Sample Output 3

Copy

958681902

题解：
只有两行，简单题哈，就不多解释了.
定义F[i]为前i列的方案数
我们可以先压缩一下，s[i]=s[i+1]的缩成一个
可以开始讨论：
如果s1[i]==s2[i] & s1[i-1]==s2[i-1]  F[i]=F[i-1]*2        i-1固定后，i有两种方案对应
        s1[i]==s2[i] & s1[i-1]!= s2[i-1]  F[i]=F[i-1]           表示i这个位置和i-1一一对应 
        s1[i]!= s2[i] & s1[i-1]==s2[i-1]  F[i]=F[i-1]*2
        s1[i]!= s2[i] & s1[i-1]!= s2[i-1]  F[i]=F[i-1]*3       都不相同时有三种方案对应，可以手画下

 #include <algorithm>
 #include <iostream>
 #include <cstdlib>
 #include <cstring>
 #include <cstdio>
 #include <cmath>
 using namespace std;
 const int N=,mod=;
 char s1[N],s2[N];long long f[N];
 void work()
 {
     int l,n=;
     scanf("%d",&l);
     scanf("%s",s1+);
     scanf("%s",s2+);
     for(int i=;i<=l;i++){
         if(s1[i]!=s1[i+]){
             s1[++n]=s1[i];
             s2[n]=s2[i];
         }
     }
     if(s1[]==s2[])f[]=;
     else f[]=;
     for(int i=;i<=n;i++){
         if(s1[i]==s2[i]){
             if(s1[i-]!=s2[i-])f[i]+=f[i-];
             else f[i]+=(f[i-]+f[i-])%mod;
         }
         else{
             if(s1[i-]==s2[i-])f[i]+=(f[i-]+f[i-])%mod;
             else f[i]+=(f[i-]*)%mod;
         }
         f[i]%=mod;
     }
     printf("%lld\n",f[n]);
 }

 int main()
 {
     work();
     return ;
 }