[BZOJ]3527 力(ZJOI2014)

　　第一次背出FFT模板，在此mark一道裸题。

Description

　　给出n个数qi，给出Fj的定义如下：

　　

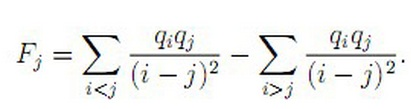
　　令Ei=Fi/qi，求Ei。

Input

　　第一行一个整数n。

　　接下来n行每行输入一个数，第i行表示qi。

Output

　　n行，第i行输出Ei。与标准答案误差不超过1e-2即可。

Sample Input

　　5
　　4006373.885184
　　15375036.435759
　　1717456.469144
　　8514941.004912
　　1410681.345880

Sample Output

　　-16838672.693
　　3439.793
　　7509018.566
　　4595686.886
　　10903040.872

HINT

　　n ≤ 100000，0 < qi < 1000000000。

Solution

　　看到题目中 下标为j的项等于下标为i的项与下标为j±i的项的乘积之和，你应该会有所感觉吧。

　　设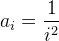，那么 。

　　显然两边都是卷积的式子，所以两边分别做一次FFT就可以了。

　　然而我们再思考一下，发现两边的式子是可以合并的：

　　设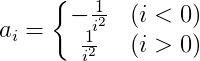，那么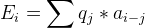 就完全成立了。只要做一次FFT就够了。

　　时间复杂度O(nlogn)。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define pi acos(-1)
#define MN 263005
using namespace std;
struct cp
{
    double v,i;
    friend cp operator+(const cp& a,const cp& b) {return (cp){a.v+b.v,a.i+b.i};}
    friend cp operator-(const cp& a,const cp& b) {return (cp){a.v-b.v,a.i-b.i};}
    friend cp operator*(const cp& a,const cp& b) {return (cp){a.v*b.v-a.i*b.i,a.v*b.i+a.i*b.v};}
}w[][MN],A[MN],B[MN],C[MN];
double a[MN];
int r[MN];
int N,n;

void init(int n)
{
    register int i,j,k;
    for (N=;N<=n;N<<=); cp g=(cp){cos(pi*/N),sin(pi*/N)};
    for (i=j=;i<N;r[++i]=j)
        for (k=N>>;(j^=k)<k;k>>=);
    w[][]=w[][]=(cp){,};
    for (i=;i<N;++i) w[][i]=w[][i-]*g;
    for (i=;i<N;++i) w[][i]=w[][N-i];
}

void FFT(cp* a,bool g)
{
    register int i,j,k;
    for (i=;i<N;++i) if (r[i]<i) swap(a[i],a[r[i]]);
    for (i=;i<N;i<<=)
        for (j=;j<N;j+=(i<<))
            for (k=;k<i;++k)
            {
                cp x=a[i+j+k]*w[g][N/(i<<)*k];
                a[i+j+k]=a[j+k]-x;
                a[j+k]=a[j+k]+x;
            }
    if (g) for (i=;i<N;++i) a[i].v/=N,a[i].i/=N;
}

int main()
{
    register int i;
    scanf("%d",&n);
    for (i=;i<=n;++i) scanf("%lf",&a[i]),A[i].v=a[i];
    for (i=;i<n;++i)
        B[n+i].v=(double)/i/i,B[n-i].v=(double)-/i/i;
    init(n<<);
    FFT(A,); FFT(B,);
    for (i=;i<N;++i) C[i]=A[i]*B[i];
    FFT(C,);
    for (i=;i<=n;++i) printf("%.7lf\n",C[n+i].v);
}

Last Word

　　推荐miskcoo的关于学习FFT的blog：从多项式乘法到快速傅里叶变换。