时间序列分解-STL分解法

时间序列分解-STL分解法

【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

Ljt

作为一个初学者，水平有限，欢迎交流指正。

---

STL(’Seasonal and Trend decomposition using Loess‘ )是以鲁棒局部加权回归作为平滑方法的时间序列分解方法。

其中Loess(locally weighted scatterplot smoothing,LOWESS or LOESS)为局部多项式回归拟合，是对两维散点图

进行平滑的常用方法，它结合了传统线性回归的简洁性和非线性回归的灵活性。当要估计某个响应变量值时，先从其预

测变量附近取一个数据子集，然后对该子集进行线性回归或二次回归，回归时采用加权最小二乘法，即越靠近估计点的

值其权重越大，最后利用得到的局部回归模型来估计响应变量的值。用这种方法进行逐点运算得到整条拟合曲线。

Robust Loess 为鲁棒局部加权回归，具体算法可以参看之前的博文 鲁棒局部加权回归 。

STL对异常点具有健壮性，仅能处理加法模式的分解，对于乘法模式需要先转换为加法模式处理最后在逆变换回去。

鲁棒局部加权回归法方法的LOESS 过程和鲁棒性过程分别在STL 的内部环 和外部环中嵌套实现．

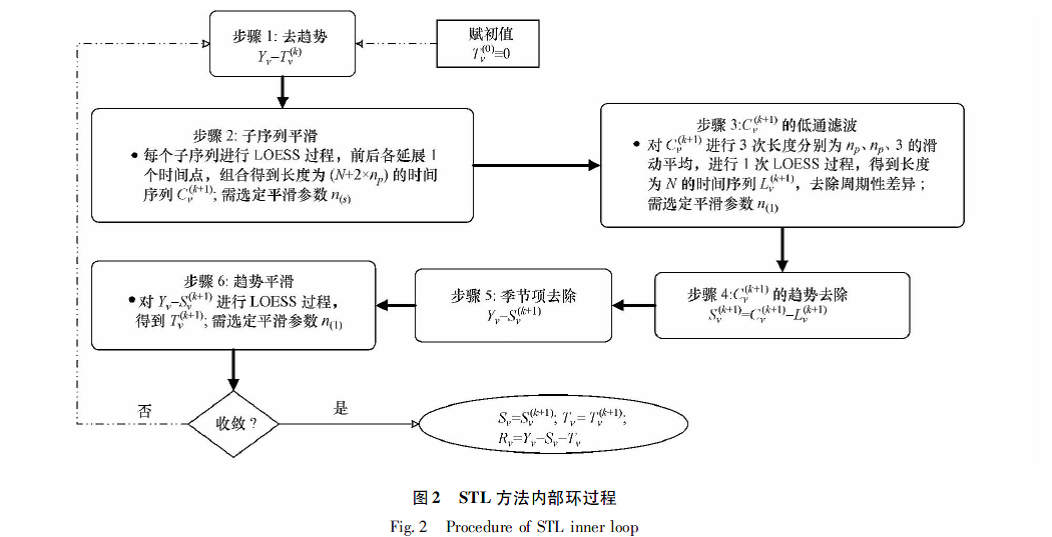
用R做时间序列的STL分解：

stl(x, s.window, s.degree = 0,
             t.window = NULL, t.degree = 1,
             robust = FALSE,
             na.action = na.fail)
        s.window----提取季节性时的loess算法时间窗口宽度，须为奇数

s.degree -----提取季节性时局部拟合多项式的阶数，须为0或1

t.window----提取趋势性时的loess算法时间窗口宽度，须为奇数

t.degree-----提取趋势性时局部拟合多项式的阶数，须为0或1

robust -----在loess过程中是否使用鲁棒拟合

library(quantmod)
###时间序列STL分解法######
##STL是’Seasonal and Trend decomposition using Loess‘ 的以鲁棒局部加权回归作为平滑方
#法的时间序列分解方法。其中Loess(locally weighted scatterplot smoothing,
#LOWESS or LOESS)为局部多项式回归拟合。
getSymbols('^IXIC',src='yahoo',from='2008-1-1',to='2015-10-1')
sdata.month=to.monthly(IXIC)
sdata.close=sdata.month$IXIC.Close
head(sdata.close)
sdata=ts(as.double(sdata.close),frequency=12,start=c(2008,1))
#as.double(sdata.close)为避免出现‘只允许单变量序列’的报错
fit=stl(sdata,t.window=13,s.window='periodic',robust=T)
#时间序列的STL分解是以鲁棒局部加权回归作为平滑方法的时间序列分解方法
#故应使robust=T，s.window='periodic'指使用均值平滑季节性子序列
plot(fit)

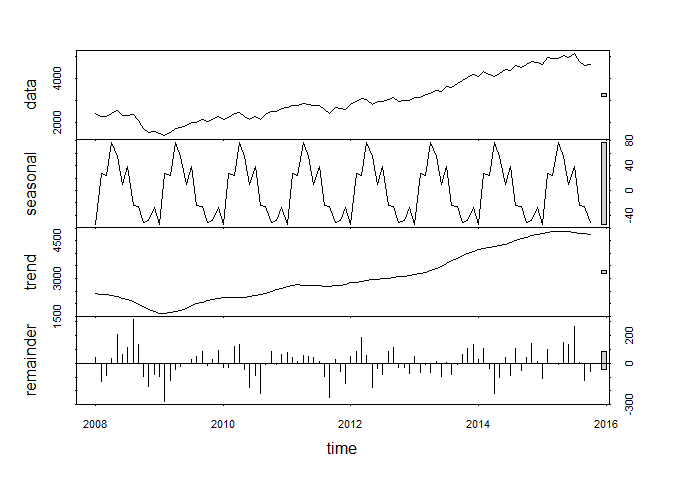
(上图4个板块的最右侧的高度不等的灰色柱条对应各板块数值大小的一个可视化度量，它们对应的数值大小是一样的）