第一页纸定义了损失函数的样子, theta, X 和 y 的 shape, 以及最终的损失函数向量表现形式．



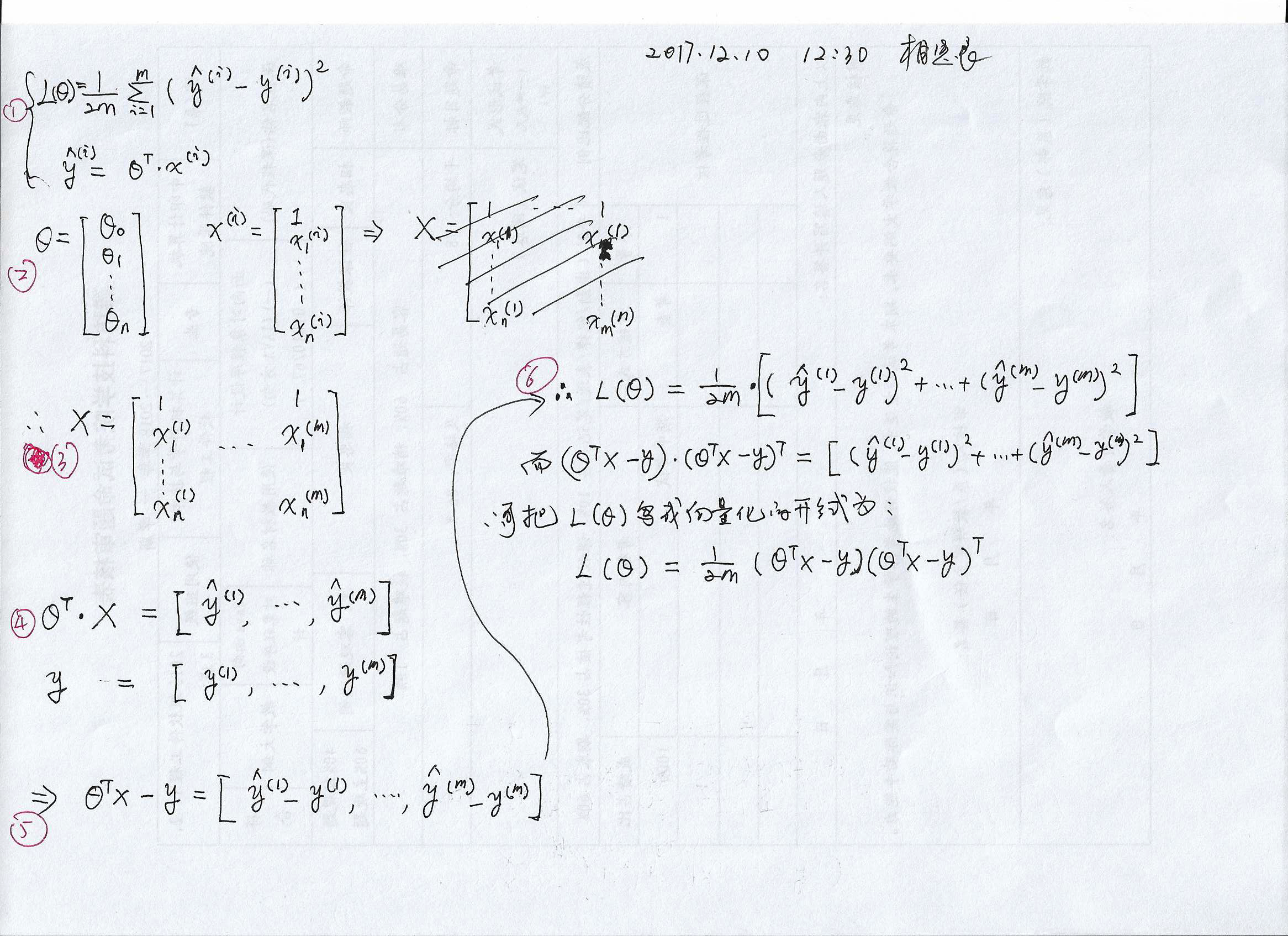
第二页纸抄上了几个要用到的矩阵求导公式，以及推导过程和结果．

要说明的是：推导结果与theta, X 和 y 的 shape有直接关系．也就是说可能和某教材，某大牛教学视频的结论外貌上不一致，但实质完全相同．

线性回归(Linear Regression)均方误差损失函数最小化时关于参数theta的解析解的推导(手写)的更多相关文章

  1. 斯坦福CS229机器学习课程笔记 Part1：线性回归 Linear Regression

    机器学习三要素 机器学习的三要素为:模型.策略.算法. 模型:就是所要学习的条件概率分布或决策函数.线性回归模型 策略:按照什么样的准则学习或选择最优的模型.最小化均方误差,即所谓的 least-sq ...

  2. ML 线性回归Linear Regression

    线性回归 Linear Regression MOOC机器学习课程学习笔记 1 单变量线性回归Linear Regression with One Variable 1.1 模型表达Model Rep ...

  3. 机器学习方法：回归（一）：线性回归Linear regression

    欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 开一个机器学习方法科普系列:做基础回顾之用,学而时习之:也拿出来与大家分享.数学水平有限,只求易懂,学习与工 ...

  4. 机器学习 (一) 单变量线性回归 Linear Regression with One Variable

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...

  5. Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable

    原文:http://blog.csdn.net/abcjennifer/article/details/7700772 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...

  6. 机器学习（三）--------多变量线性回归(Linear Regression with Multiple Variables)

    机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables) 同样是预测房价问题  如果有多个特征值 那么这种情况下  假设h表示 ...

  7. Ng第二课：单变量线性回归(Linear Regression with One Variable)

    二.单变量线性回归(Linear Regression with One Variable) 2.1  模型表示 2.2  代价函数 2.3  代价函数的直观理解 2.4  梯度下降 2.5  梯度下 ...

  8. 斯坦福第二课：单变量线性回归(Linear Regression with One Variable)

    二.单变量线性回归(Linear Regression with One Variable) 2.1  模型表示 2.2  代价函数 2.3  代价函数的直观理解 I 2.4  代价函数的直观理解 I ...

  9. 机器学习 (二) 多变量线性回归 Linear Regression with Multiple Variables

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...

随机推荐

  1. OpenID Connect + OAuth2.0

    一.问题的提出 现代应用程序或多或少都是如下这样的架构: 在这种情况下,前端.中间层和后端都需要进行验证和授权来保护资源,所以不能仅仅在业务逻辑层或者服务接口层来实现基础的安全功能.为了解决这样的问题 ...

  2. ELK学习总结（3-2）elk的过滤查询

    和一般查询比较,filter查询:能够缓存数据在内存中,应该尽可能使用 建立测试数据 查看测试数据 1.filtered查询 GET /store/products/_search { "q ...

  3. python入门（1）python的前景

    python入门(1)python的前景 Python是一种解释型.面向对象.动态数据类型的高级程序设计语言. Python由Guido van Rossum于1989年底发明,第一个公开发行版发行于 ...

  4. testNG常用方法

    1.常用注释: 注解                  描述 @BeforeSuite                       在该套件的所有测试都运行在注释的方法之前,仅运行一次. @After ...

  5. 转：java中Vector的使用

    转:https://www.cnblogs.com/zhaoyan001/p/6077492.html Vector 可实现自动增长的对象数组. java.util.vector提供了向量类(vect ...

  6. Spring Boot面试题

    Spring Boot 是微服务中最好的 Java 框架. 我们建议你能够成为一名 Spring Boot 的专家. 问题一 Spring Boot.Spring MVC 和 Spring 有什么区别 ...

  7. SQL优化（SQL TUNING）之10分钟完成亿级数据量性能优化（SQL调优）

    前几天,一个用户研发QQ找我,如下: 自由的海豚. 16:12:01 岛主,我的一条SQL查不出来结果,能帮我看看不? 兰花岛主 16:12:10 多久不出结果? 自由的海豚 16:12:17 多久都 ...

  8. Java基础语法<五> 大数值BigInteger BigDecimal

    笔记整理 来源于<Java核心技术卷 I > <Java编程思想> 如果基本的整数和浮点数精度不能够满足需求,那么可以使用java.math包中的两个很有平有用的类:BigIn ...

  9. nginx 官方文档翻译

    nginx(发音为"engine x")是一个由俄罗斯软件工程师Igor Sysoev编写的免费开源Web服务器.自2004年公开发布以来,nginx专注于高性能,高并发性和低内存 ...

  10. Windows下安装Python3和Django

    下载python3 首先去 python的官网 下载最新稳定版的python3, 我下载的时候python3的最新版本是3.6.5. 亦可点击 此链接 直接下载. 安装python3 傻瓜式安装,注意 ...