zh.wikipedia.org/wiki/凸優化

以下问题都是凸优化问题，或可以通过改变变量而转化为凸优化问题：[5]

Convex function

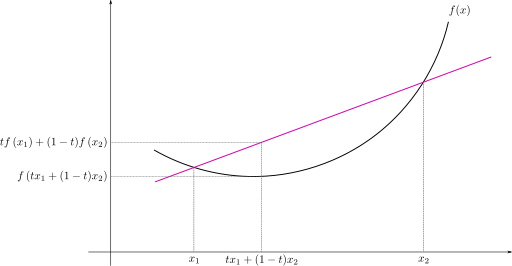
Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets. The convexity makes optimization easier than the general case since local minimum must be a global minimum, and first-order conditions are sufficient conditions for optimality.[1]

https://web.stanford.edu/~boyd/cvxbook/

Convex optimization 凸优化的更多相关文章

  1. CMU Convex Optimization(凸优化)笔记1--凸集和凸函数

    CMU凸优化笔记--凸集和凸函数 结束了一段时间的学习任务,于是打算做个总结.主要内容都是基于CMU的Ryan Tibshirani开设的Convex Optimization课程做的笔记.这里只摘了 ...

  2. 凸优化(Convex Optimization)浅析

    本博客已经迁往http://www.kemaswill.com/, 博客园这边也会继续更新, 欢迎关注~ 在机器学习中, 很多情况下我们都需要求得一个 问题的全局最优值(global optimum) ...

  3. 凸优化 Convex Optimization PDF 扫描文字识别版

    凸优化理论 Convex Optimization 清华大学出版社 王书宁许窒黄晓霖译 Stephen Boyd Lieven Vandenbergt原著 2013 年l 月第1 版 下载链接 链接: ...

  4. 在线学习和在线凸优化（online learning and online convex optimization）—FTL算法5

    最自然的学习规则是使用任何在过去回合中损失最小的向量. 这与Consistent算法的精神相同,它在在线凸优化中通常被称为Follow-The-Leader,最小化累积损失. 对于任何t: 我们谈到了 ...

  5. 在线学习和在线凸优化（online learning and online convex optimization）—凸化方法4

    一些在线预测问题可以转化到在线凸优化框架中.下面介绍两种凸化技术: 一些在线预测问题似乎不适合在线凸优化框架.例如,在线分类问题中,预测域(predictions domain)或损失函数不是凸的.我 ...

  6. 凸优化简介 Convex Optimization Overview

    最近的看的一些内容好多涉及到凸优化,没时间系统看了,简单的了解一下,凸优化的两个基本元素分别是凸函数与凸包 凸集 凸集定义如下: 也就是说在凸集内任取两点,其连线上的所有点仍在凸集之内. 凸函数 凸函 ...

  7. 在线学习和在线凸优化（online learning and online convex optimization）—在线凸优化框架3

    近年来,许多有效的在线学习算法的设计受到凸优化工具的影响. 此外,据观察,大多数先前提出的有效算法可以基于以下优雅模型联合分析: 凸集的定义: 一个向量 的Regret定义为: 如前所述,算法相对于竞 ...

  8. 在线学习和在线凸优化（online learning and online convex optimization）—在线分类问题2

    紧接上文,我们讲述在线分类问题 令,为0-1损失,我们做出如下的简化假设: 学习者的目标是相对于hypotheses set: H具有low regret,其中H中的每个函数是从到{0,1}的映射,并 ...

  9. 在线学习和在线凸优化（online learning and online convex optimization）—基础介绍1

    开启一个在线学习和在线凸优化框架专题学习: 1.首先介绍在线学习的相关概念 在线学习是在一系列连续的回合(rounds)中进行的: 在回合,学习机(learner)被给一个question:(一个向量 ...

随机推荐

  1. vue笔记一

    一.Vue基本知识点 1.声明式渲染 <div id="app">{{ msg }}</div> <script> var app = new ...

  2. Django的Form、CSRF、cookie和session

    Django是一个大而全的web框架,为我们提供了很多实用的功能,本文主要介绍Form.CSRF.cookie和session 一.Form 在web页面中form表单是重要的组成部分,为了数据安全和 ...

  3. foreach 加& 什么意思？

    foreach 加&遍历的同时改变原数组即修改数据或者增加数据 foreach 加& 什么意思? 注意:如果我要改变数组某一个值 直接遍历的话原数组是不会变的 下面提供两种方法 1.我 ...

  4. _.pick lodash

    http://lodash.think2011.net/pick _.pick(object, [props]) 创建一个从 object 中选中的属性的对象. 参数 object (Object) ...

  5. kettle入门(七) 之kettle增量方案(一)全量比对取增量-依据唯一标示

    引: ods有个project表来自于上游系统,数据量不大 十几万,下游系统须要此数据,而且须要每天提供截止当天的增量数据 要求每条数据给出数据变化时间及标示,即数据若是插入 有插入时间和插入标示 若 ...

  6. 【Excle数据透视表】如何调整压缩形式显示下的缩进字符数

    调整前:                                                                                                 ...

  7. spring 源码下载

    github spring 源码 导入Spring源码方法 java世界中的三大构建工具:ant,maven,gradle gradle 简介

  8. windows远程桌面如果超出最大连接数, 使用命令行mstsc /console登录即可

    远程桌面如果超出最大连接数, 使用命令行mstsc /console登录即可. (也可以用 mstsc /admin) 可以在运行里使用mstsc /console /v:IP:远程端口即可强制登录; ...

  9. 如果你报createSQLQuery is not valid without active transaction,请看这里

    原文:https://blog.csdn.net/yinjian520/article/details/8666695 很多时候我们使用hibernate的session时,都是让session在某一 ...

  10. NSAttributedString设置行间距，间接设置了uilabel的行间距

    假设有UIlabel实例:_testLabel NSString * testString = @"明月当空,隐隐约约听到低吟,似有若无.面对大千世界的奢华糜烂,还不如在这一方小城,静静品一 ...