GBDT的数学原理

一、GBDT的原理

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。
  GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。
  GBDT的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合。业界中，Facebook使用其来自动发现有效的特征、特征组合，来作为LR模型中的特征，以提高CTR预估（Click-Through Rate Prediction）的准确性（详见参考文献5、6）；GBDT在淘宝的搜索及预测业务上也发挥了重要作用（详见参考文献7）。

提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数时平方损失和指数损失函数时，每一步的优化很简单，如平方损失函数学习残差回归树。

但对于一般的损失函数，往往每一步优化没那么容易，如上图中的绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。（注：鄙人私以为，与其说负梯度作为残差的近似值，不如说残差是负梯度的一种特例）算法如下（截图来自《The Elements of Statistical Learning》）：

算法步骤解释：

• 1、初始化，估计使损失函数极小化的常数值，它是只有一个根节点的树，即ganma是一个常数值。
• 2、
  （a）计算损失函数的负梯度在当前模型的值，将它作为残差的估计
  （b）估计回归树叶节点区域，以拟合残差的近似值
  （c）利用线性搜索估计叶节点区域的值，使损失函数极小化
  （d）更新回归树
• 3、得到输出的最终模型 f(x)

二、GBDT的参数设置

1、推荐GBDT树的深度：6；（横向比较：DecisionTree/RandomForest需要把树的深度调到15或更高）

2、【问】xgboost/gbdt在调参时为什么树的深度很少就能达到很高的精度？
  用xgboost/gbdt在在调参的时候把树的最大深度调成6就有很高的精度了。但是用DecisionTree/RandomForest的时候需要把树的深度调到15或更高。用RandomForest所需要的树的深度和DecisionTree一样我能理解，因为它是用bagging的方法把DecisionTree组合在一起，相当于做了多次DecisionTree一样。但是xgboost/gbdt仅仅用梯度上升法就能用6个节点的深度达到很高的预测精度，使我惊讶到怀疑它是黑科技了。请问下xgboost/gbdt是怎么做到的？它的节点和一般的DecisionTree不同吗？

【答】

（1）Boosting主要关注降低偏差（bais），因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成；Bagging主要关注降低方差（variance），因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。
（2）随机森林(random forest)和GBDT都是属于集成学习（ensemble learning)的范畴。集成学习下有两个重要的策略Bagging和Boosting。
  Bagging算法是这样做的：每个分类器都随机从原样本中做有放回的采样，然后分别在这些采样后的样本上训练分类器，然后再把这些分类器组合起来。简单的多数投票一般就可以。其代表算法是随机森林。Boosting的意思是这样，他通过迭代地训练一系列的分类器，每个分类器采用的样本分布都和上一轮的学习结果有关。其代表算法是AdaBoost, GBDT。
（3）其实就机器学习算法来说，其泛化误差可以分解为两部分，偏差（bias)和方差(variance)。这个可由下图的式子导出（这里用到了概率论公式D(X)=E(X^2)-[E(X)]^2）。偏差指的是算法的期望预测与真实预测之间的偏差程度，反应了模型本身的拟合能力；方差度量了同等大小的训练集的变动导致学习性能的变化，刻画了数据扰动所导致的影响。这个有点儿绕，不过你一定知道过拟合。
  如下图所示，当模型越复杂时，拟合的程度就越高，模型的训练偏差就越小。但此时如果换一组数据可能模型的变化就会很大，即模型的方差很大。所以模型过于复杂的时候会导致过拟合。
  当模型越简单时，即使我们再换一组数据，最后得出的学习器和之前的学习器的差别就不那么大，模型的方差很小。还是因为模型简单，所以偏差会很大。

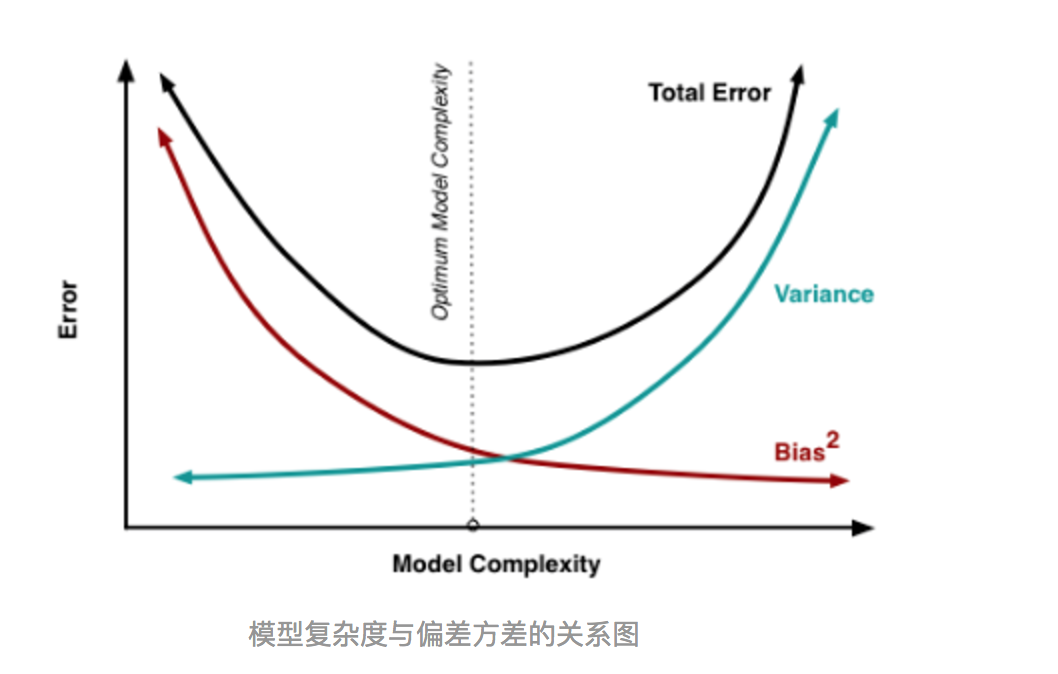
也就是说，当我们训练一个模型时，偏差和方差都得照顾到，漏掉一个都不行。
  对于Bagging算法来说，由于我们会并行地训练很多不同的分类器的目的就是降低这个方差(variance) ,因为采用了相互独立的基分类器多了以后，h的值自然就会靠近.所以对于每个基分类器来说，目标就是如何降低这个偏差（bias),所以我们会采用深度很深甚至不剪枝的决策树。
  对于Boosting来说，每一步我们都会在上一轮的基础上更加拟合原数据，所以可以保证偏差（bias）,所以对于每个基分类器来说，问题就在于如何选择variance更小的分类器，即更简单的分类器，所以我们选择了深度很浅的决策树。

三、参考文献

1、http://www.jianshu.com/p/005a4e6ac775