4.4清北学堂Day1 主要内容：数论，数学

Day 1;

1、常见的高精

1. 输入输出都用字符数组；
2. 字符数组的实际长度用strlen()来求；
3. 运算时倒序运算，把每一个字符都-‘0’

1. 进位的处理上也要注意；
   1. 小数减大数时先判断大小然后加负号
   2. 
   3. 只能用while不能用if    因为if只能去掉一个0，while去掉所有的前导零

高精减：

高精乘；

通过逐位相乘，进完位之后输出

2、特殊处理

高精数除以单精数

压位技巧：

把对十取模变成了%10000或者更长，对加和减没啥用，但是乘除的时候能够大量提高速度，复杂度为o(n/m);

在int下可以最多压9位，能够很好的减少时间

2、模意义下运算

模7意义下的运算

模意义下运算这一块比较难，主要还是日后求逆元的时候比较费劲

3*3=2  4+5=2  4-5=6

即3*3 mod 7=2

无除法运算（但可以用逆元来代替）

满足基本的交换律、分配率、结合律

对中间结果取模不影响最终答案 ；

5*5*5 mod 7 = 6

(5*5 mod 7)^5 mod 7 = 4*5 mod 7

快速幂

计算a^b%p=?

暴力O(b)

两种解决思路：

分治

分治代码pow(a,b)%c

快速幂

快速幂代码

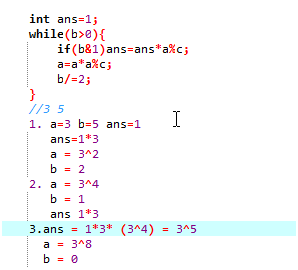
b&1指二进制下b的第一位

费马小定理

t=b*a^(p-1)=b

t=b*1=b

/a=*a^(p-2);

用费马小定理的方法来代替/a;

PS!!!!!

O(1)计算组合数：

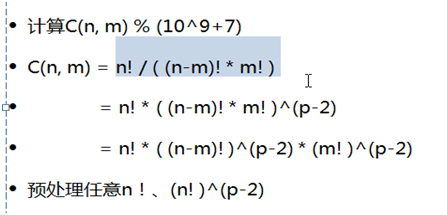
第三步进行了拆分，把两个阶乘拆开了

最后发现组合数只与n！、（n！）^(p-2)

一个很省时间的模板。。。。。。但是不习惯用

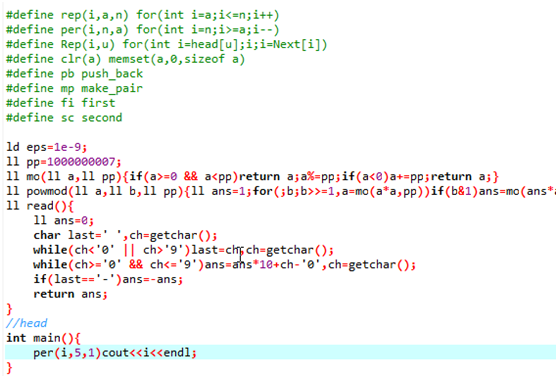
#define  clr(a)  memset(a,0,sizeof(a))

清零

Ps：快读比scanf快4倍左右

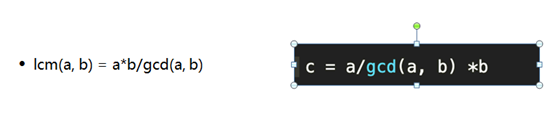
GCD和LCM

没什么可讲的，唯一注意的是用GCD求LCM要注意顺序。。。。前一种有可能会爆

筛素数

弱智筛法就不贴了

下面是埃氏筛

先补一个很有意思的东西

1+1/2+1/3+1/4+....+1/n=log n

线性筛代码

欧拉函数

对于大范围内求质因数个数硬解肯定太慢，用线性筛优化

先用线性筛找到每一个数的最小质因子(rec[i])

分析：第二个if里，当i的指数>=2时就可以直接乘，（主要是看rec[i]对于phi[i]的贡献,例如一次幂二次幂等）当指数>2时，说明i因数分解式当中有多个该质因子，那么我们就可以直接相乘。

例如：

36=2^2*3^2

Phi[36]=phi[18]*2

=2*1*3*2=6;=12

18=2*3^2

Phi[18]=2^(1-1)           *    (2-1)    *    3^(2-1)           *    (3-1)

=1*1*3*2=6;

否则在(i/rec[i])基础上乘该数最小质因子的欧拉函数（即rec[i]-1）。

例如phi[15]和phi[30]

Phi[15]=(3-1)*(5-1)=8

Phi[30]=(2-1)* (3-1)*(5-1)=8

=phi[30/2]*(2-1)=8

通过对欧拉函数的应用，我们可以慢慢的发现这条定理：

欧拉定理

矩阵

1、

• 一个m×n的矩阵就是m×n个数排成m行n列的一个数阵
• 一个m×p的矩阵A 乘 一个一个p×n的矩阵B 得到一个矩阵一个m×n的矩阵AB
• 其中
• 

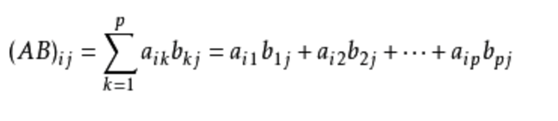
乘法的时候，第i行第j列就等于原本两个矩阵里头前矩阵i行和后矩阵j列全部元素对应相乘

• 注意！矩阵乘法满足结合律、分配率
• 不满足交换律

应用：

求斐波那契数列第k项的值

Fi表示斐波那契第i项

0 1    f1  f2              f2

1 1    f2  f1+f2         f3

0 1     K-1次幂   f1     fk

1 1         f2   fk+1

代码实现

ans起初是单位矩阵

计算f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4) 的第k项

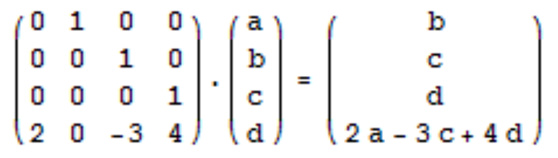
套模板，先找一个矩阵看能不能使得前矩阵通过运算变成后矩阵，可以通过在前（n-1）行用01来求解，最后一行按题目要求的系数填入的方法

邻接矩阵

表示第i行的点能不能到第j个点上

比如

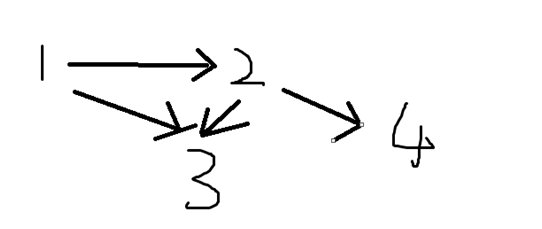
可以得到

0 1 1 0

0 0 1 1

0 0 0 0

0 0 0 0

矩阵的k次幂表示走几步能到达

高斯消元

1、         应用场景：解齐次线性方程组

例：

解齐次线性方程

2x + y - z = 8

-3x - y + 2z = -11

-2x + y + 2z = -3

可以得到

2    1    -1   8

-3   -1   2    -11

-2   1    2    -3

常规的高斯消元法只需要循环（或者递归）求解即可

有一个很重要的区别

行列式消元的时候，当a[i][i]==0的时候，对该列进行交换；

矩阵消元的时候，当a[i][i]==0的时候，则i++；

代码实现：

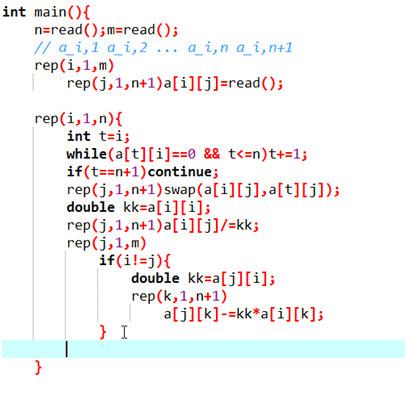
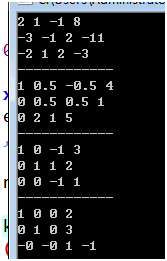
行列式    emmmm其实应该在矩阵前头啊

1.把齐次线性方程组的矩阵拿出来构成一个行列式，若值为0则无解或无穷多解，非0则有解

2.解法：用高斯消元消成上三角就行，或者降阶求解

矩阵逆元：

若矩阵B*A=I则称B为A的左逆元

有逆元的前提：矩阵行列式不为0

求左逆元：对于A矩阵的第二行减去第一行，其实就是对于一个换单位矩阵在单独的某一行进行系数变换

左逆元其实就是高斯消元过程中的矩阵连乘

同理，右逆元是对列进行系数变换

矩阵树定理

• 一个图的邻接矩阵G：对于无向图的边(u,v)，G[u][v]++,G[v][u]++

一个图的度数矩阵（有多少条边与之相连，那么他的度数就是多少）D：对于无向图的边(u,v)，D[u][u]++,D[v][v]++

• 而通过这两个矩阵就可以构造出图G的基尔霍夫矩阵：C=D-G.
• Matrix Tree定理：将图G的基尔霍夫矩阵去掉第i行和第i列(i可以取任意值，可以证明所得到的结果相同)，得到(n-1)*(n-1)的矩阵，对这个矩阵进行行列式的值求解，abs(det(A))即为图G的生成树个数。