Tree POJ - 1741【树分治】【一句话说清思路】

因为该博客的两位作者瞎几把乱吹(〃￣︶￣)人(￣︶￣〃)用彼此的智慧总结出了两条全新的定理（高度复杂度定理、特异根特异树定理），转载请务必说明出处。（逃

Pass：anuonei，anuonei，我感觉大部分人都不需要这些东西吧，当初研究是因为看不懂别人的博客……还有，有些性质在dalao们看起来是相当显然，但我们真的不懂啊，讨论到深更半夜的说。定理都非严格证明，因为我们有点困了（逃）。其实都是闹着玩的，主要是自己开心兴奋自豪懂了就好啦，还望大家都以过家家的心态来看这些中二爆棚的话，以鼓励代批评啦qwq。

深く感謝しております！q(≧▽≦q)

“树简直TM就是为分治而生的!，万岁！”

1）本题思路：（请结合下一个板块

1、  树上所有路径都有相同形式：某个可以成为某子树根的节点+其子孙们

2、  本题的路径查询可以化简为只有一个变量，设u为i、j的父亲或祖先，u合法是dis[i]+dis[j]<=k且i、j节点属于不同子树，u不合法是dis[i]+dis[j]<=k且i、j节点属于同一子树，则有：

u全部=u合法+u不合法

u不合法=u子树合法

最后两层节点所构成的子树有：全部=合法（没有不合法的）

所以有公式如下：

根合法

=根全部-根不合法

=根全部-子树合法

=根全部-子树全部-子树不合法

=根全部-子树全部-子子树合法

=根全部-子树全部-子子树全部-……-最后一棵树全部

具体细节全在代码里

感谢https://blog.csdn.net/bahuia/article/details/53066373

2）笔者结合该题对分治算法的理解如下：

一句话，这道题（或说分治算法）其实就是dfs树，唯一的改进之处就是以平衡点递归而非dfs序，（由高度复杂度定理我们知这会带来更高效率）。又由特异根特异树定理我们知道，同一坨树，定根不同，子树不同，所以每找到一个新的平衡点（newroot），之前储存的其麾下子树性质不再正确，所以每次再找平衡点子树的平衡点前都要再求一遍子树性质（logN），求平衡点用去复杂度logN*logN。

每层复杂度O（n），高度复杂度定理知总复杂度N*logN*logN。

3）定理说明以及补充：

1））此题为该论文例1：（感谢高中生dalao ，从小到大没受过这么大委屈இ௰இ）https://wenku.baidu.com/view/e087065f804d2b160b4ec0b5.html

2））高度复杂度定理：树这个数据结构拥有更高效率，用树优化的方法的复杂度与高度成正比，等于单层复杂度之和*高度，所以完全树的效率优化最明显，这道题执着于求平衡点就是为了降低高度。

我们以归并排序来解释该定理（请不要觉得多此一举没必要看，万一帮助很大呢(´▽`ʃ♡ƪ)）

前置技能，图片也来源于此：https://www.cnblogs.com/chengxiao/p/6194356.html

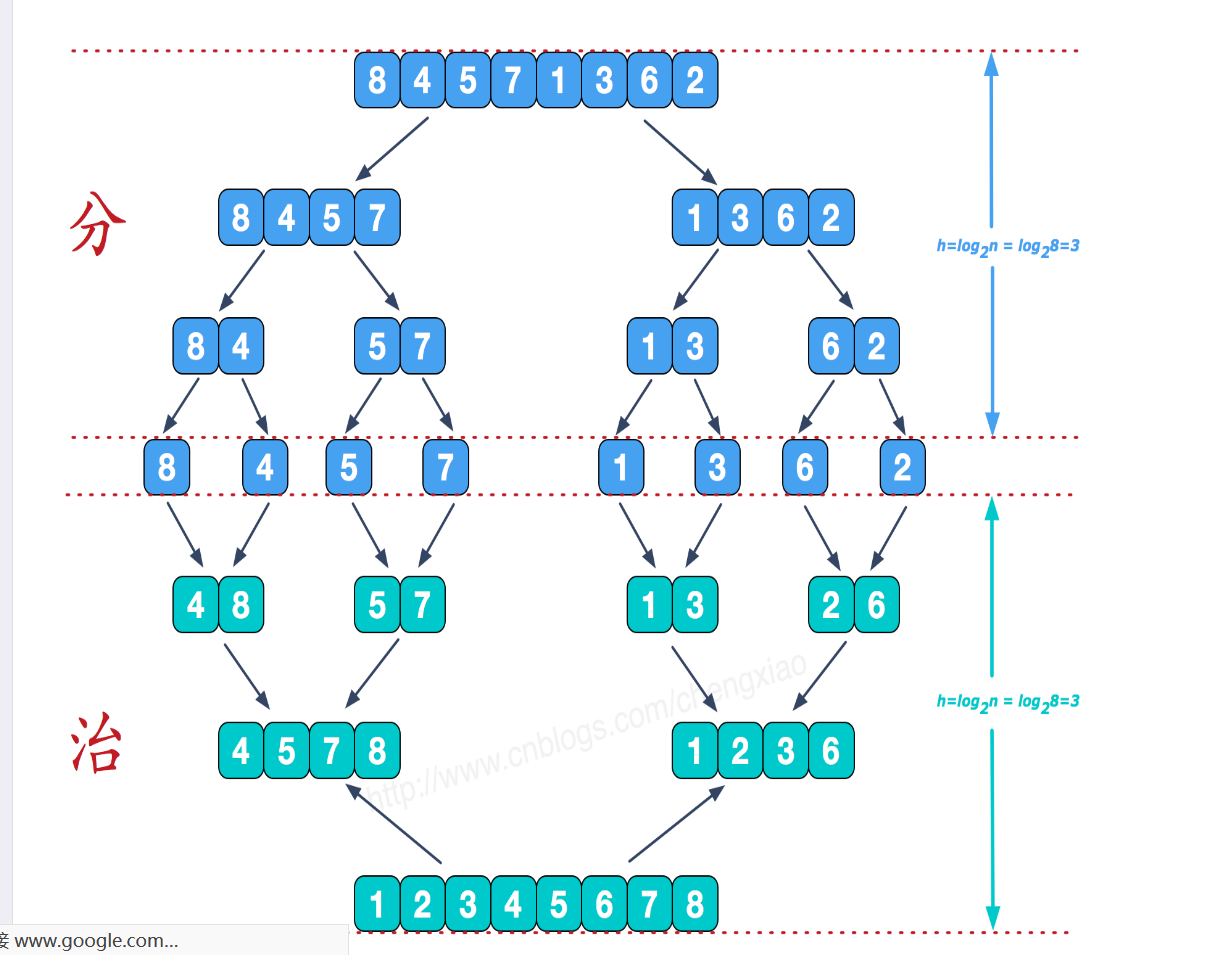
 一句话解释：

总复杂度为各节点复杂度之和，对于归并排序来说，各层复杂度之和恒等于N，对于其他情况，我们依然假设此前提成立（我知道这样不严谨，但也许错得不是很离谱，是依然有实践意义的吧，求指教），所以总复杂度=N*logN（每层排序复杂度N*高度）

 

数学递推证明：

T（n）=f（n）+2T（n/2）= n+2T（n/2）

2T（n/2）=2（f（n/2）+2T（n/4））=2（n/2+2T（n/4））

……

2T（2）=2（f（2）+2T（1）=2（2+2T（1））

以上各式累加得：

T（n）=n+n+……+n（logn个）=nlogn

 

3））特异根特异树定理：对于一棵树，定根不同，子树不一定相同。

public class Tree {
    static IO io = new IO();
    static final int maxn = 10100, inf = Integer.MAX_VALUE / 100;
    static int N, K, cnt, ans;

    static class Edge {
        int v, next, cost;

        public Edge(int v, int next, int cost) {
            this.v = v;
            this.next = next;
            this.cost = cost;
        }
    }

    static Edge[] edges = new Edge[maxn * 2];
    static int[] head = new int[maxn];

    public static void main(String[] args) {
        while (true) {
            N = io.nextInt();
            K = io.nextInt();
//            可读性呼吁(～￣(OO)￣)ブ，|&都是些什么鬼，难看死了
//            本来就是搞不懂才会去搜别人的代码的
            if (N == 0 && K == 0) return;
            cnt = 0;
            Arrays.fill(head, -1);
            for (int i = 0; i < N - 1; i++) {
                int a = io.nextInt(), b = io.nextInt(), c = io.nextInt();
                add(a, b, c);
                add(b, a, c);
            }
            Arrays.fill(vis, false);
//            重要！！：在递归方法里修改的变量：
//            如需要的结果可能是中间结果（newroot），或回溯修改（ans），或全程起某种左右（minmaxchild）
//            为确保万无一失，都请务必全局化
//            ans即使使用java的Integer传参数也会导致错误结果（至于为什么，求指教qwq
            ans = 0;
            dfs(1);
            io.println(ans);
        }
    }

    //    单层复杂度=logn+logn+nlogn=nlogn，总复杂度=nlogn*logn
    static boolean[] vis = new boolean[maxn];
//　　　　　　pre防止通过双向边往上
//　　　　　　定根newroot后，已经处理过的点会变成newroot的孙子，vis[]防止遍历跑出子树
    static void dfs(int u) {
        minmaxchild = inf;
        getsize(u, -1);
        getnewroot(u, u, -1);
        int newr = newroot;
//        加上以newr为根的树全部
//        以newroot！！！！！！！！！！！！！！！
//        以newroot！！！！！！！！！！！！！！！
//        以newroot！！！！！！！！！！！！！！！
        ans += call(newr, 0);
        vis[newr] = true;
        for (int i = head[newr]; i != -1; i = edges[i].next)
            if (!vis[edges[i].v]) {
//                等价于减去以u为根的树不合法
//                等价于减去以u为根的子树合法
//                newroot递归会变，我可不希望循环着循环着错位了
                ans -= call(edges[i].v, edges[i].cost);
                dfs(edges[i].v);
            }
    }

    //    以u为根，从上到下普通的dfs遍历树，
//    size[i]存的是，以u为根的树中，以i为根的子树大小
//    maxchild[i]存的是，以u为根的树中，以i为根的所以子树里最大子树的大小
    static int[] size = new int[maxn];
    static int[] maxchild = new int[maxn];

    //    复杂度logn*常数=logn
    static int getsize(int u, int pre) {
        size[u] = 1;
        maxchild[u] = 0;
        for (int i = head[u]; i != -1; i = edges[i].next)
            if (!vis[edges[i].v] && edges[i].v != pre) {
                size[u] += getsize(edges[i].v, u);
                maxchild[u] = Math.max(maxchild[u], size[edges[i].v]);
            }
        return size[u];
    }

    //    以u为根，从上到下普通的dfs遍历树，
//    在这个过程中，顺便找出了newroot
//    minmaxchild是一个中间变量，是用来筛newroot的标准，不保存，但要初始化
//    以防万一，按照前面约定好的，minmaxchild设为全局
//    其意义是：（依然以u为根），u子树的各个节点分别为newroot时，
//    每个newroot的最大子树大小里，最小的那个，也是最平衡的那个
    static int minmaxchild, newroot;

    //    复杂度logn*常数=logn
    static void getnewroot(int r, int u, int pre) {
//        若以u为平衡点newroot，
//        我们希望其最大子树越接近总结点数的一半
        if (minmaxchild > Math.max(maxchild[u], size[r] - maxchild[u])) {
            minmaxchild = Math.max(maxchild[u], size[r] - maxchild[u]);
            newroot = u;
        }
        for (int i = head[u]; i != -1; i = edges[i].next)
            if (!vis[edges[i].v] && edges[i].v != pre)
                getnewroot(r, edges[i].v, u);
    }

    //    一次call算出整颗u根树的全部
//    dis存的是u根树里所有节点到根的距离
    static ArrayList<Integer> dis = new ArrayList<Integer>();

    //    复杂度nlogn+n=nlogn
    static int call(int u, int d) {
//        遍历复杂度n
        dis.clear();
        filldis(u, d, -1);
//        排序复杂度nlogn
        Collections.sort(dis);
        int i = 0, j = dis.size() - 1, ret = 0;
        while (i < j) {
            while (i < j && dis.get(i) + dis.get(j) > K) j--;
            ret += j - i;
            i++;
        }
        return ret;
    }

    //    复杂度n
    static void filldis(int u, int d, int pre) {
//        把add操作放第一行让我避免了一些细节上的处理
        dis.add(d);
        for (int i = head[u]; i != -1; i = edges[i].next)
            if (!vis[edges[i].v] && edges[i].v != pre)
                filldis(edges[i].v, edges[i].cost + d, u);
    }

    static void add(int a, int b, int c) {
        edges[cnt] = new Edge(b, head[a], c);
        head[a] = cnt++;
    }