【数学建模】偏最小二乘回归分析（PLSR）

PLSR的基本原理与推导，我在这篇博客中有讲过。

0.
偏最小二乘回归集成了多元线性回归、主成分分析和典型相关分析的优点，在建模中是一个更好的选择，并且MATLAB提供了完整的实现，应用时主要的问题是：

• 注意检验，各种检验参数：有关回归的检验以及有关多元分析的检验
• 系数众多，容易混淆
• 要清楚原理才能写好论文
• 注意matlab函数plsregress的众多返回值
• 例如累计贡献度，建模时最好列出表格

1.

问题：

自变量组 X = [x1,x2…xn]  （n组自变量）

因变量组 Y = [y1,y2,…yp]   （p组因变量）

考虑到X、Y内部之间的多重相关性，可以使用PLSR建立Y对X的多元回归模型。这是一种多对多回归的模型。

偏最小二乘回归的实现步骤：

1. X、Y标准化。若考虑标准化的不对等特性，考虑实现对应分析。
2. 求相关系数矩阵。可以把X、Y统一放到一个增广矩阵中，实现求列向量之间的相关系数矩阵（corrcoef实现无需标准化，直接使用原始数据）
3. 求主成分对。（求出自变量与因变量的成分，类似于典型相关分析）这里对数其实是min(n-1,p)。求出<u1,v1>、<u2,v2>… 实际上，u、v是原始变量标准化后的线性组合、即投影。
4. 计算贡献率表格。计算前k个主成分u对原始变量X的贡献率、v对Y的贡献率（函数直接返回结果）。
5. 根据贡献率表格，选取k个主成分对。一般累计贡献率达到90%合适。
6. 求出原始变量X对这k个主成分u的回归方程以及Y对u的（不是v！）回归方程。
7. 根据6的结果，可以求出因变量组Y与自变量组X的回归方程，但这其实是标准化了的（常数项一定是0），进一步可以还原为真实原始变量的回归方程，这也是我们所要求得的。
8. 模型的解释与检验。

• • 首先得进行一个回归检验：判定系数R方的检验（接近于1)。计算每一个回归方程的R方，可以列出表格。
  • 之后进行交叉有效性检验：交叉系数Qh方 = 1 – （PRESS(h) / SS(h-1)）。这是从主成分分析的角度的检验，即检验提取的k个主成分。（这个检验比较复杂，详细看推导）

2.

MATLAB实现命令：

[XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] = plsregress(X,Y,ncomp)

param:

　　X: 标准化后的原始X数据，每行一个数据组，每列是一项指标，即一个自变量

　　Y：标准化后的原始Y数据，每行一个数据组，每列是一项指标，即一个因变量

　　ncomp：选取的主成分对数

return：

　　XL：自变量的负荷量矩阵。维度是（自变量数*ncomp）。每行是原始数据X对主成分u的回归表达式的系数

　　YL：因变量的负荷量矩阵。维度是（自变量数*ncomp）。每行是原始数据Y对主成分u的回归表达式的系数

　　XS：对应于主成分u的得分矩阵(得分说的是主成分的值)。每列是一个主成分得分向量。

　　　　如：每一列是一个主成分ui的值！列数是主成分数。

　　　　说明:主成分u1是个列向量.

　　YS：对应于主成分v的得分矩阵。每列是一个v对原始数据Y的线性组合的系数

　　BETA：最终的回归表达式系数矩阵。每一列对应的，是一个yi对X的回归表达式系数。

　　PCTVAR：两行的矩阵。

　　　　第一行的每个元素代表着自变量提出主成分，相应主成分u的贡献率。（特征值之比，详细见主成分推导）

　　　　第二行的每个元素代表着因变量提出主成分，相应主成分v的贡献率。这个贡献率其实是主成分对原始变量的解释能力大下。

　　MSE：两行的矩阵。剩余标准差矩阵。第一行的第j个元素对应着自变量与他的前j-1个提出成分之间的剩余标准差。第二行对应因变量。

　　stats：返回4个值。结构体：stats。

　　    W — A p-by-ncomp matrix of PLS weights so that XS = X0*W.

　　　　    W = a\XS。 W每行是一个主成分得分向量的系数，如：

　　    T2 — The T2 statistic for each point in XS.

　　    Xresiduals — The predictor residuals, that is, X0-XS*XL'.

　　    Yresiduals — The response residuals, that is, Y0-XS*YL'.

3.

案例实现：

求Y对X的偏最小二乘回归方程：

原始数据：

(前三列为X变量，后两列为Y变量，共20组样本。以下数据保存为pz.txt与matlab源文件同一文件夹下)

 % PLSR 偏最小二乘

 clc,clear
  ab0 = load('pz.txt');
  mu = mean(ab0);%均值
 sig = std(ab0);% 标准差
 rr = corrcoef(ab0) %相关系数矩阵
 ab = zscore(ab0); %数据标准化
 a = ab(:,[:]); %标准化的X
  b = ab(:,[:end]); %标准化的Y
  % pls命令需要标准化变量
 [XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] = plsregress(a,b)
  contr = cumsum(PCTVAR,) %每行累计求和，即计算累计贡献率
 XL
  YL
  XS
  YS
  xw = a\XS %自变量提出主成分系数，每列对应一个成分,这个就是stats.W
  yw = b\YS %因变量提出的主成分系数
 ncomp = input('输入主成分个数')
 [XL2,YL2,XS2,YS2,BETA2,PCTVAR2,MSE2,stats2] = plsregress(a,b,ncomp)
  n = size(a,);% n是自变量个数
 m = size(b,);
  %求原始数据回归方程常数项
 beta3(,:) = mu(n+:end) - mu(:n)./sig(:n)*BETA2([:end],:).*sig(n+:end);
  %求原始数据x1,x2...xn的系数，每一列是一个回归方程
 beta3([:n+],:) = (./sig(:n))'*sig(n+1:end).*BETA2([2:end],:)
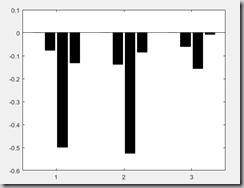
  bar(BETA2','k') %画直方图

求解结果（部分）

假设采用2个主成分

ncomp =

2

系数：
XL2 =

-4.1306    0.0558
    -4.1933    1.0239
     2.2264    3.4441

YL2 =

2.1191   -0.9714
     2.5809   -0.8398
     0.8869   -0.1877

主成分得分（每列一个主成分）：
XS2 =

-0.1036   -0.2050
    -0.1241   -0.0577
    -0.1463    0.1807
     0.1110    0.2358
    -0.0785   -0.3927
    -0.0369    0.0249
    -0.2263    0.0263
     0.1199    0.0730
     0.2765    0.2263
     0.1874   -0.0577
     0.0588   -0.2428
     0.1198   -0.2420
     0.1913    0.2625
    -0.7077    0.2635
    -0.1327   -0.3375
    -0.1208    0.1803
    -0.0633    0.0707
     0.1933   -0.2712
     0.1690   -0.1291
     0.3131    0.3917

YS2 =

-1.2834    0.1794
    -4.6311    1.3388
    -0.2845   -0.6256
    -1.2265    0.6851
     1.6002   -1.0788
    -4.5120    1.5408
    -2.9777   -0.0114
    -2.7548    1.5473
     3.9469   -0.4253
    10.4846   -2.6373
     1.4139   -0.6681
     4.8549   -1.1547
     5.2890   -1.0550
    -7.6800   -0.1989
    -5.1793    1.2090
     4.5405   -2.0460
    -6.4973    2.0374
     4.2728   -0.6046
     5.5489   -1.3537
    -4.9251    3.3215

标准化数据回归方程系数（可以看到常数项系数是0）
BETA2 =

0.0000    0.0000    0.0000
    -0.0773   -0.1380   -0.0603
    -0.4995   -0.5250   -0.1559
    -0.1323   -0.0855   -0.0072

贡献率：
PCTVAR2 =

0.6948    0.2265
     0.2094    0.0295

剩余标准差：
MSE2 =

2.8500    0.8699    0.2242
     2.8500    2.2531    2.1689

stats2 =

W: [3x2 double]
             T2: [20x1 double]
     Xresiduals: [20x3 double]
     Yresiduals: [20x3 double]

最终的回归方程系数矩阵，每列一个方程:
beta3 =

47.0375  612.7674  183.9130
    -0.0165   -0.3497   -0.1253
    -0.8246  -10.2576   -2.4964
    -0.0970   -0.7422   -0.0510

画出回归系数直方图：

还可以用预测的方法做精度分析，在此略过。