Python 实现 动态规划 /斐波那契数列

1、斐波那契数列

　　斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(3)=2,F(n)=F(n-1)+F(n-2)（n>=4，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

　　（1）、递归算法 （三点：  终止条件（边界），最优子结构 F(1)=1，F(2)=1, F(3)=2,F(n)=F(n-1)+F(n-2)  状态转移公式  F(n)=F(n-1)+F(n-2)）

def fab(n):
    # 终止条件 边界
    if n <= 2:
        return 1
    else:
        # 最优子结构 状态转移公式
        return fab(n - 1) + fab(n - 2)

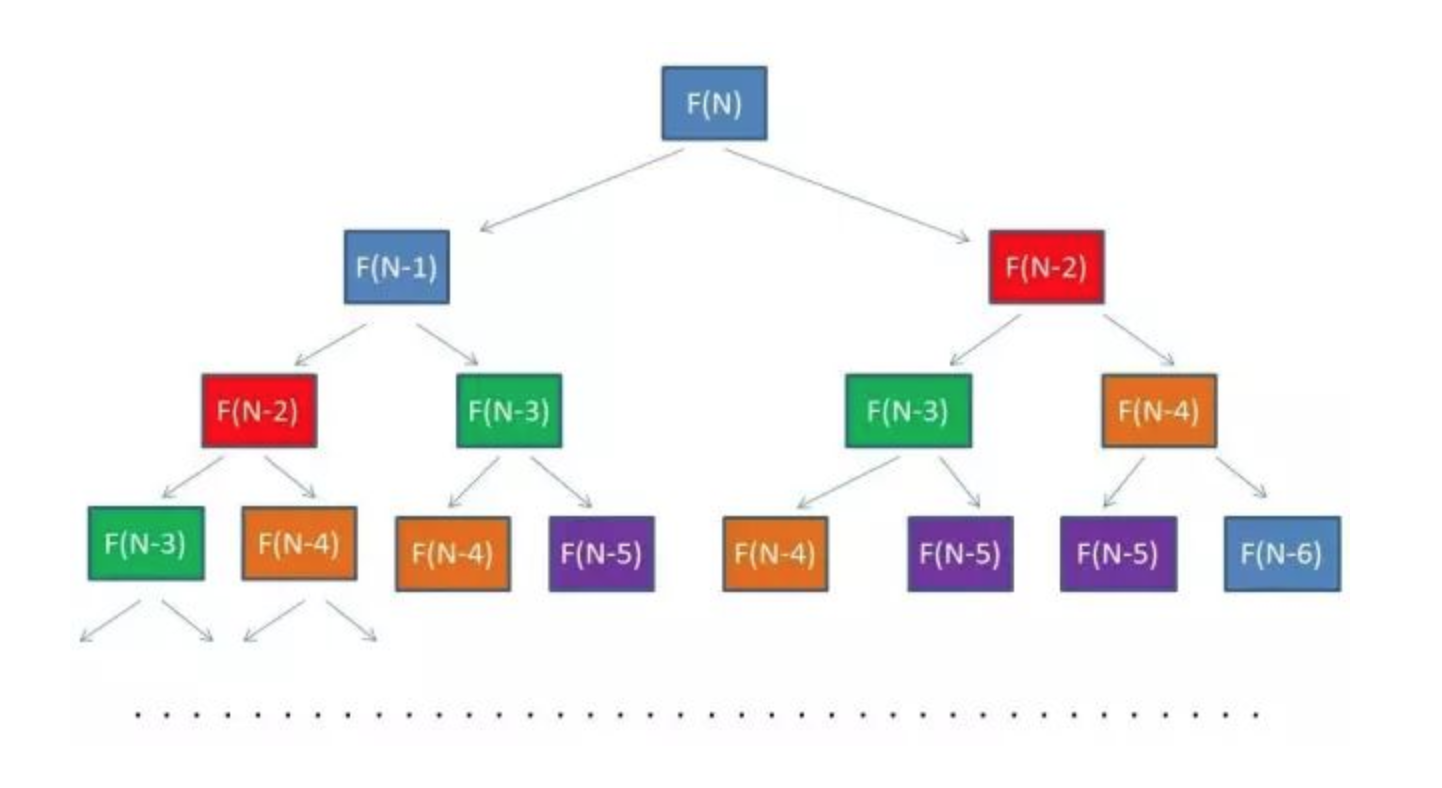
　　（2）、优化  递归算法 会重复计算多次同一个式子 如图 相同的颜色代表了方法被传入相同的参数。所以需要记录下已经计算过得数，防止重复计算

# 记录已经计算过得 值
dict_fab = {}

def fab_2(n):
    # 终止条件 边界
    if n <= 2:
        return 1
    elif dict_fab.get(n):
        print('*')
        return dict_fab.get(n)
    else:
        # 最优子结构 状态转移公式
        dict_fab[n] = fab_2(n - 1) + fab_2(n - 2)
        return dict_fab[n]

　　（3）、动态规划

# 最终优化 动态规划  （大问题化成若干相同类型的子问题 然后一个个解决子问题）
def fab_3(n):
    # 由前往后推
    a = 1
    b = 1
    if n <= 2:
        print('fab({})={}'.format(n, b))
        return 1
    for i in range(n - 2):
        print(a, b)
        a, b = b, a + b
    print('fab({})={}'.format(n, b))
    return b

2、盛水问题 Python解法（题目链接https://leetcode.com/problems/trapping-rain-water/description/ ）

　　（1）、暴力解法

　　

def trap(height):
    sum_water = 0
    size = len(height)
    for i in range(size):
        max_left = 0
        max_right = 0
        for j in range(0, i + 1):
            max_left = max(max_left, height[j])
        for j in range(i, size):
            max_right = max(max_right, height[j])
        sum_water += min(max_left, max_right) - height[i]
    return sum_water

　　（2）、动态规划（记忆算法，记录i 位置的左右 最大数，减少for循环层级 时间复杂度 有o（n²）变为 o(n)）

def trap_water_dy():
    height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
    sum_water = 0
    size = len(height)
    max_left_lsit = [None]*size
    max_left_lsit[0] = height[0]
    max_right_list = [None]*size
    max_right_list[-1] = height[-1]

    for i in range(1, size):
        max_left_lsit[i] = max(height[i], max_left_lsit[i - 1])

    for i in range(size-1):
        max_right_list[size - 2 - i] = max(height[size - 2 - i], max_right_list[size - i - 1])

    for i in range(size):
        sum_water += min(max_left_lsit[i], max_right_list[i]) - height[i]
    return sum_water

（3）、双指针

def trap_two_point():
    height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
    left = 0
    right = len(height) - 1
    ans = 0
    left_max = 0
    right_max = 0
    while left < right:  # 循环数组一遍
        if height[left] < height[right]:  # 当左边的小于右边的 能装多少水 由左边的最高高度决定
            if height[left] >= left_max:
                left_max = height[left]
            ans += (left_max - height[left])
            left += 1
        else:  # 当右边小于左边时 装的水量由右边的最高高度决定
            if height[right] >= right_max:
                right_max = height[right]
            ans += (right_max - height[right])
            right -= 1
    return ans