0x11栈之火车进栈

参考《算法竞赛进阶指南》p.49

题目链接：https://www.acwing.com/problem/content/description/131/

递推与递归的宏观描述

对于一个待求解的问题”，当它局限在某处边界、某个小范围或者某种特殊情形时，其答案往往是已知的。如果能够将该解答的应用场景扩大到原问题的状态空间，且扩展过程的每个步骤具有相似性，就可以考虑使用递推或者递归求解。以已知的“问题边界”为起点向“原问题”正向推导的扩展方式就是递推。然而在很多时候，推导路线难以确定，这时以“原问题”为起点尝试寻找把状态空间缩小到已知的“问题边界”的路线，再通过该路线反向回溯的遍历方式就是递归。我们通过两幅图来表示递推与递归的差别。

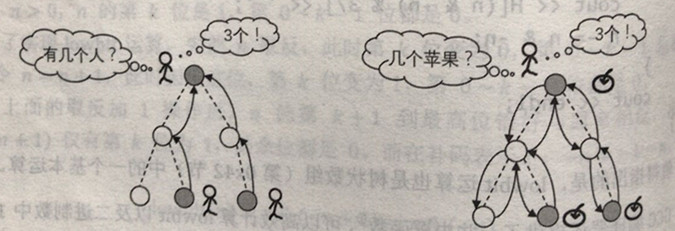
左侧图中，有几个人是原问题，从原问题往前推导是递推。于是从二叉树的最后一层往前推，推导到第一层则可以算出原问题的答案。

右侧图中，几个苹果是原问题。但是在这棵二叉树中，你并不知道有几层和结点的分布情况。对每一个子问题都是一颗二叉树，遍历左右子数，求出苹果，然后往回返回苹果数目。我们刚才也提到，使用递推或递归要求“原问题”与“问题边界”之间的每个变换步骤具有相似性，这样我们才能够设计一段程序实现这个步骤，将其重复作用于问题之中。换句话说，程序在每个步骤上应该面对相同种类的问题，这些问题都是原问题的一个子问题，可能仅在规模或者某些限制条件上有所区别，并且能够使用“求解原问题的程序”进行求解。

对于递归算法，有了上面这个前提，我们就可以让程序在每个变换步骤中执行三个操作:

1.缩小问题状态空间的规模。这意味着程序尝试寻找在“原问题”与“问题边界”之间的变换路线，并向正在探索的路线上迈出一步。

2.尝试求解规模缩小以后的问题，结果可能是成功，也可能是失败。

3.如果成功，即找到了规模缩小后的问题的答案，那么将答案扩展到当前问题，如果失败，那么重新回到当前问题，程序可能会继续寻找当前问题的其他变换路线，直至最终确定当前问题无法求解。

在以上三个操作中有两点颇为关键。-是“如何尝试求解规模缩小以后的问题”。因为规模缩小以后的问题是原问题的一个子问题，所以我们可以把它视为一个新的“原问题”由相同的程序(上述三个操作)进行求解，这就是所谓的“自身调用自身”。二是如果求解子问题失败，程序需要重新回到当前问题去寻找其他的变换路线，因此把当前问题缩小为子问题时所做的对当前问题状态产生影响的事情应该全部失效，这就是所谓的“回溯时还原现场”。上面这类程序就是“递归”的遍历方式，其整体流程如下图所示。

可以看到，递归程序的基本单元是由“缩小”“求解” “扩展” 组成的种变换步骤，只是在“求解”时因为问题的相似性，不断重复使用了这样一种变换步骤， 直至在已知的问题边界上直接确定答案。对于其中任意一条从“原问题”到“问题边界”的变换路线(图中实线圈出的路径)，横向来看，它的每层是次递归程序体的执行；纵向来看，它的左右两边分别是寻找路线和沿其推导的流程。为了保证每层的“缩小”与“扩展”能够衔接在同形式的问题上，“求解” 操作自然要保证在执行前后程序面对问题的状态是相同的，这也就是“还原现场”的必要性所在。

对于题目中问题：

面对任何一个状态我们只有两种选择：

1.把下一个数进栈

2.把当前栈顶元素出栈

先进行第二步操作比第一步操作的字典序小。

import java.util.LinkedList;
import java.util.Scanner;
import java.util.Stack;

public class Main {
	static LinkedList<Integer> list=new LinkedList<Integer>();
	static Stack<Integer> stack=new Stack<Integer>();
	static LinkedList<Integer> ans=new LinkedList<Integer>();
	static int cnt=20;
	static int n=0;
	static void dfs() {
		if (cnt==0) {
			return;
		}
		if (ans.size()==n) {
			for (Integer integer : ans) {
				System.out.print(integer);
			}
			System.out.println();
			cnt--;
			return;
		}

		if (stack.size()!=0) {
			int x=stack.pop();
			ans.add(x);
			dfs();
			//System.out.println(ans.peekLast()==x);
			stack.push(x);
			ans.removeLast();

		}
		if (list.size()!=0) {
			int s=list.getLast();
			list.removeLast();
			stack.push(s);
			dfs();
			list.add(s);
			stack.pop();
		}
	}
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		n=sc.nextInt();
		for (int i = n; i >=1; i--) {
			list.add(i);
		}
		dfs();
	}

}