Codeforces Round #317 [AimFund Thanks-Round] (Div. 2) Minimization dp

原题链接：http://codeforces.com/contest/572/problem/D

题意

给你个数组A和n,k，问你排列A后，下面的最小值是多少。

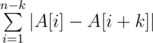
题解

先排个序，要填充像1,1+k,1+2k,1+3k....这样的序列，或像2,2+k,2+2k.......这样的序列，这些序列应该取排序数组中连续的一段才能使得答案最小，现在考察这些序列的大小，发现其大小要么是n/k，要么是n/k+1，所以可以dp[i][j]表示前 i 条序列我取了 j 个n/k这样的序列。转移就很简单了，详见代码。

代码

#include <bits/stdc++.h>

using namespace std;

long long dp[][];
int n, k, a, b, x, y, z[];

long long inf = 1e18;

int main() {
    //freopen("in.in", "r", stdin);
    //freopen("out.out", "w", stdout);
    while (scanf("%d %d", &n, &k) != EOF) {
        for (int i = ; i <= n; i++)
            scanf("%d", &z[i]);
        sort(z + , z + n + );
        x = n / k;
        y = n / k + ;
        b = n - k * x;
        a = k - b;
        dp[][] = z[y] - z[];
        dp[][] = z[x] - z[];
        for (int i = ; i <= a + b; i++) {
            for (int j = ; j <= min(a, i); j++) {
                if (i == j) {
                    dp[i][j] = dp[i - ][j - ] + (long long)z[(i - ) * x + x] - z[(i - ) * x + ];
                }
                else {
                    int tmp = j * x + (i -  - j) * y;
                    if (tmp + y <= n) dp[i][j] = dp[i - ][j] + (long long)z[tmp + y] - z[tmp + ];
                    else dp[i][j] = inf;
                    if (j > ) {
                        tmp = (j - ) * x + (i - j) * y;
                        if (tmp + x <= n)
                            dp[i][j] = min(dp[i][j], dp[i - ][j - ] + (long long)z[tmp + x] - z[tmp + ]);
                    }
                }
            }
        }
        //for (int i = 1; i <= 3; i++) printf("--> %I64d\n", dp[i][i]);
        printf("%I64d\n", dp[a + b][a]);
    }
    return ;
}