各大排序

图论：

　　spfa

　　floyd

　　dijkstra

　　*拉普拉斯矩阵

hash表

拓扑排序

哈夫曼算法

匈牙利算法

分块法

二分法

费马小定理：

　　a^(p-1) ≡1（mod p）

网络流

二分图

后缀数组

倍增算法

RMQ

并查集

∑求和符号：连这符号都不认得就别玩竞赛了。。。

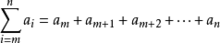
组合数：

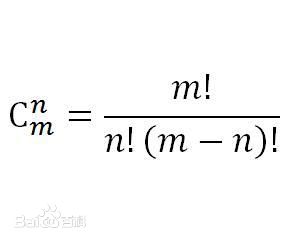
排列数：

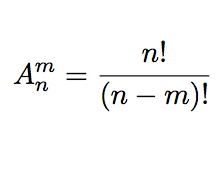
　　排列数中有重复元素的全排列：M!/(N1!*N2!*...*Nn!)

memset奇淫技巧：

　　memset(A,0x7f,sizeof(A));初始化为最大值INF=2139062143

　　memset(A,0x8f,sizeof(A));初始化为最小值INF=-1886417009

　　memset(A,-1,sizeof(A));初始为-1

　　memset(A,0,sizeof(A));初始为0//感觉这个有点多余，应该所有人都知道吧

容斥原理：

|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|

Catalan序列：C(n,2n)/（n+1）

欧拉函数：

先占坑。。。

OI算法复习汇总的更多相关文章

  1. OI算法复习

    搜集一些算法,赛前背一背有好处的 转自各大网站 前排感谢:hzwer.风了咕凉 前辈...Orz 快速读入: int read() { ,f=;char ch=getchar(); ;ch=getch ...

  2. Java 算法 概念汇总

    编程面试的10大算法概念汇总   以下是在编程面试中排名前10的算法相关的概念,我会通过一些简单的例子来阐述这些概念.由于完全掌握这些概念需要更多的努力,因此这份列表只是作为一个介绍.本文将从Java ...

  3. C#冒泡算法复习

    C#冒泡算法复习 冒泡算法的意思:每一趟找到一个最小或最大的数放到最后面,比较总数的n-1次(因为比较是2个双双比较的) 第一层循环表示进行比较的次数,总共要比较(数的)-1次 (因为比较是2个双双比 ...

  4. lua学习之复习汇总篇

    第六日笔记 1. 基础概念 程序块 定义 在 lua 中任何一个源代码文件或在交互模式中输入的一行代码 程序块可以是任意大小的 程序块可以是一连串语句或一条命令 也可由函数定义构成,一般将函数定义写在 ...

  5. c++常考算法知识点汇总

    前言:写这篇博客完全是给自己当做笔记用的,考虑到自己的c++基础不是很踏实,只在大一学了一学期,c++的面向对象等更深的知识也一直没去学.就是想当遇到一些比较小的知识,切不值得用一整篇 博客去记述的时 ...

  6. C语言排序算法复习

    排序算法有很多种,这里在复习和分析的基础上,做一个自己的总结: 首先要知道有哪些排序算法,google一下,有云C语言7大经典排序算法(也有8大).主要包括冒泡排序,快速排序,选择排序,插入排序,希尔 ...

  7. KMP算法复习【+继续学习】

    离NOIP还剩12天,本蒟蒻开始准备复习了. 先来个KMP[似乎我并没有写过KMP的blog] KMP KMP算法是解决字符串匹配问题的一个算法,主要是单对单的字符串匹配加速,时间复杂度O(m + n ...

  8. 算法复习周------“动态规划之‘最长公共子序列’”&&《计蒜课》---最长公共子串题解

    问题描述: 这个问题其实很容易理解.就是给你两个序列X={x1,x2,x3......xm} Y={y1,y2,y3......ym},要求找出X和Y的一个最长的公共子序列. 例:Xi={A, B, ...

  9. K-Means聚类和EM算法复习总结

    摘要: 1.算法概述 2.算法推导 3.算法特性及优缺点 4.注意事项 5.实现和具体例子 6.适用场合 内容: 1.算法概述 k-means算法是一种得到最广泛使用的聚类算法. 它是将各个聚类子集内 ...

随机推荐

  1. 关于HTML5画布canvas的功能

    一.画布的使用 1.首先创建一个画布(canvas) <canvas id=”myCanvas” width=”200” height=”100” style=”border:1px solid ...

  2. js函数-构成

    前言 函数是一种封装,在任何语言中都是一个核心概念.在js中,函数是做为对象的子类型存在的.可以拥有自己的属性和方法,可以做为值进行传递,这两个特性让js拥有使用函数式编程的能力. 函数的声明 字面量 ...

  3. thinkphp5使用前置后置操作

    下面举个例子,前置删除的例子   模型事件只可以在调用模型的方法才能生效,使用查询构造器通过Db类操作是无效的   控制器中实例化类   $cate=model('cate'); $cate-> ...

  4. JavaWeb案例：上次访问时间 Cookie技术

    package cn.itcast.access; import javax.servlet.ServletException; import javax.servlet.annotation.Web ...

  5. Theme Section

    题目链接 #include <cstdio> #include <iostream> #include <cstring> using namespace std; ...

  6. 1.检索数据 ---SQL

    相关提示: 结束SQL语句 多条SQL语句必须以分号(:)分隔.多数DBMS不需要在单条SQL语句后加分号,但也有DBMS可能必须在单条SQL语句后加上分号.当然,如果愿意可以总是加上分号.事实上,即 ...

  7. GYM 101572I（有向图上最小环）

    逗号空格是假的,全都直接连边就行. 提供一个迪杰n次的图上最小环板子. #include <cstdio> #include <cstring> #include <io ...

  8. 关于Spring配置文件xml文档的schema约束

    最开始使用spring框架的时候,对于其配置文件xml,只是网上得知其使用方法,而不明其意.最近想着寻根问底的探究一下.以下是本文主要内容: 1.配置文件示例. <?xml version=&q ...

  9. 048 Rotate Image 旋转图像

    给定一个 n × n 的二维矩阵表示一个图像.将图像旋转 90 度(顺时针).注意:你必须在原矩阵中旋转图像,请不要使用另一个矩阵来旋转图像.例 1:给出的输入矩阵 = [  [1,2,3],  [4 ...

  10. 作用域提升（Scope Hositing ）是 Webpack 3 的标志性特征

    http://blog.csdn.net/playboyanta123/article/details/73533079