bzoj3624(Apio2008):免费道路
题目↓


Sample Input
1 3 0
4 5 1
3 2 0
5 3 1
4 3 0
1 2 1
4 2 1
Sample Output
4 3 0
5 3 1
1 2 1
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<ctime>
#include<map>
#define maxn 20010
#define maxm 100010
using namespace std;
struct Edge{
int u,v,w,f;
}e[maxm];
int sign[maxn],fa[maxn],n,m,k,cnt,tot;
bool cmp1(Edge x,Edge y){return x.w>y.w;}
bool cmp2(Edge x,Edge y){return x.w<y.w;}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void kruskal(int f)
{
cnt=;
for(int i=;i<=n;++i) fa[i]=i;
for(int i=;i<=m;++i){
int u=e[i].u,v=e[i].v;
int k1=find(u),k2=find(v);
if(k1!=k2){
if(f){
if(e[i].w<){
if(tot<k) tot++;
else continue;
}
e[i].f=;
}
else if(!e[i].w) continue;
fa[k1]=k2;
++cnt;
}
if(cnt+==n) return;
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i=;i<=m;++i) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
sort(e+,e+m+,cmp1);
kruskal();
cnt=;
for(int i=;i<=n;++i){
if(fa[i]==i){
cnt++;
sign[i]=;
}
}
if(cnt->k){
puts("no solution");
return ;
}
for(int i=;i<=m;++i) if(!e[i].w) if(sign[e[i].u]||sign[e[i].v]) e[i].w=-;
sort(e+,e+m+,cmp2);
kruskal();
if(cnt+<n||tot!=k){
puts("no solution");
return ;
}
for(int i=;i<=m;++i) if(e[i].f) printf("%d %d %d\n",e[i].u,e[i].v,e[i].w<?:);
return ;
}
bzoj3624(Apio2008):免费道路的更多相关文章
- [BZOJ3624][Apio2008]免费道路
[BZOJ3624][Apio2008]免费道路 试题描述 输入 输出 输入示例 输出示例 数据规模及约定 见“输入”. 题解 第一步,先尽量加入 c = 1 的边,若未形成一个连通块,则得到必须加入 ...
- BZOJ3624: [Apio2008]免费道路(最小生成树)
题意 题目链接 Sol 首先答案一定是一棵树 这棵树上有一些0边是必须要选的,我们先把他们找出来,如果数量$\geqslant k$显然无解 再考虑继续往里面加0的边,判断能否加到k条即可 具体做法是 ...
- bzoj 3624: [Apio2008]免费道路 生成树的构造
3624: [Apio2008]免费道路 Time Limit: 2 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 111 Solved: 4 ...
- 题解 Luogu P3623 [APIO2008]免费道路
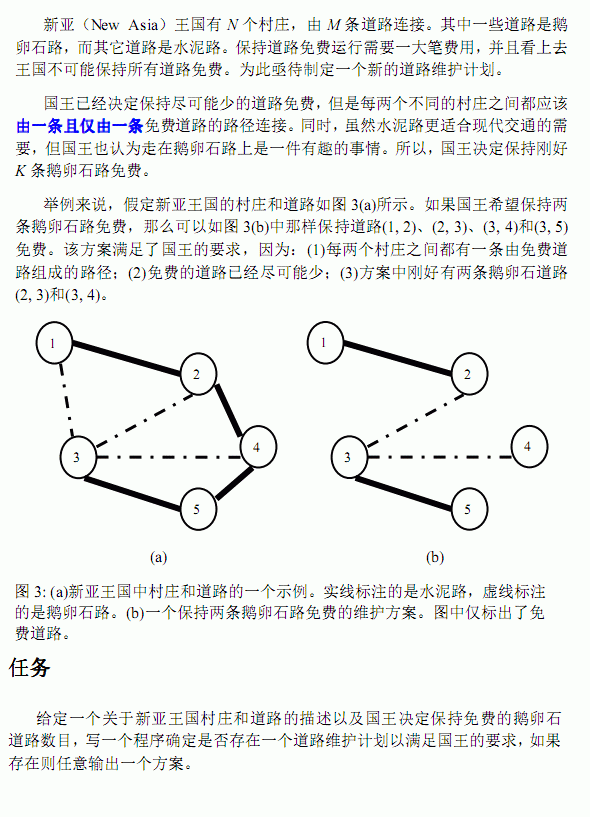
[APIO2008]免费道路 题目描述 新亚(New Asia)王国有 N 个村庄,由 M 条道路连接.其中一些道路是鹅卵石路,而其它道路是水泥路.保持道路免费运行需要一大笔费用,并且看上去 王国不可 ...
- BZOJ 3624: [Apio2008]免费道路
3624: [Apio2008]免费道路 Time Limit: 2 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 1201 Solved: ...
- [Apio2008]免费道路[Kruscal]
3624: [Apio2008]免费道路 Time Limit: 2 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 1292 Solved: ...
- P3623 [APIO2008]免费道路
3624: [Apio2008]免费道路 Time Limit: 2 Sec Memory Limit: 128 MBSec Special Judge Submit: 2143 Solved: 88 ...
- Kruskal算法及其类似原理的应用——【BZOJ 3654】tree&&【BZOJ 3624】[Apio2008]免费道路
首先让我们来介绍Krukal算法,他是一种用来求解最小生成树问题的算法,首先把边按边权排序,然后贪心得从最小开始往大里取,只要那个边的两端点暂时还没有在一个联通块里,我们就把他相连,只要这个图里存在最 ...
- [APIO2008]免费道路
[APIO2008]免费道路 BZOJ luogu 先把必须连的鹅卵石路连上,大于k条no solution 什么样的鹅卵石路(u,v)必须连?所有水泥路都连上仍然不能使u,v连通的必须连 补全到k条 ...
- [APIO2008]免费道路(生成树)
新亚(New Asia)王国有 N 个村庄,由 M 条道路连接.其中一些道路是鹅卵石路,而其它道路是水泥路.保持道路免费运行需要一大笔费用,并且看上去 王国不可能保持所有道路免费.为此亟待制定一个新的 ...
随机推荐
- MySQL数据库卸载有残留, windows10 sc delete 拒绝访问 失败5
sc delete 拒绝访问,原因是当前用户的权限不足,需要做的是在注册表 HKEY_LOCAL_MACHINE\Software\Microsoft\Windows\CurrentVersion\P ...
- QT5 文件读写操作
QFile Class 1.read读文件 加载文件对象 QFile file("文件地址"); 打开加载的文件file.open(打开方式); 操作文件 关闭打开的文件file ...
- 对深层嵌套对象进行取值&赋值
需求如下: let obj = { foo: { bar: { name: 'biz' } } }; // 输出 'biz' this.getObj(obj, 'foo.bar.name'); obj ...
- P2597 [ZJOI2012]灾难——拓扑,倍增,LCA
最近想学支配树,但是基础还是要打好了的: P2597 [ZJOI2012]灾难 这道题是根据食物链链接出一个有向图的关系,求一个物种的灭绝会连带几种物种的灭绝: 求得就是一个点能支配几个点: 如果一个 ...
- Arrays.toString的作用
Arrays.toString()的作用是用来很方便地输出数组,而不用一个一个地输出数组中的元素. 这个方法是是用来将数组转换成String类型输出的,入参可以是long,float,double,i ...
- CF786E ALT
题意 有一棵 \(n\) 个点的树和 \(m\) 个人,第 \(i\) 个人从 \(u_i\) 走到 \(v_i\) 现在要发宠物,要求一个人要么他自己发到宠物,要么他走的路径上的都有宠物. 求最小代 ...
- netcore 发布到IIS上常见错误
1 出现AspNetCoreModuleV2错误 报错原因: 你的IIS服务器上的.net core 运行时不是最新的,导致AspNetCoreModuleV2模块缺失或者报错,意思需要你更新了! 2 ...
- Oracle plsql 触发器 查询/启用/停止
在PLSQL中查询某个表的触发器脚本 select * from user_triggers where table_name='xxx' oracle触发器的启用和停用 1.禁用 table_nam ...
- [i.MX]飞思卡尔IMX6处理器的GPIO-IOMUX_PAD说明
在linux或android系统中,假如我们要配置飞思卡尔IMX6处理器的GPIO管脚,比如是GPIO_19这个管脚,那么要像这样: #define MX6Q_PAD_GPIO_19__GPIO_4_ ...
- android: 日期转Unix时间戳,Unix时间戳转日期,带时区
1.UTC时间&GMT时间 UTC时间是时间标准时间(Universal Time Coordinated),UTC是根据原子钟来计算时间,误差非常小. UTC也是指零时区的时间,如果要表示其 ...
