leetcode94 不同的二叉搜索树

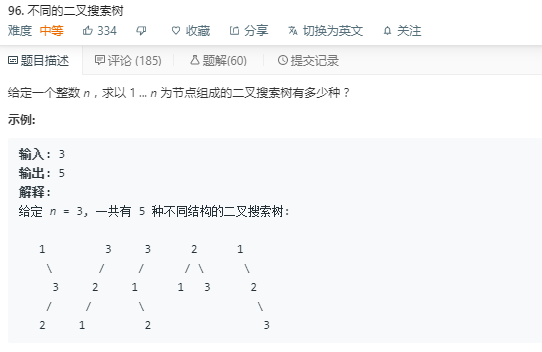
solution 1：**动态规划

class Solution {
public:
    int numTrees(int n) {
        vector<int> g={1,1,2};
        for(int i=3;i<=n;i++){
            int sum=0;
            for(int j=1;j<=i;j++){
                sum+=g[j-1]*g[i-j];
            }
            g.push_back(sum);
        }
        return g[n];
    }
};

solution 2：**数学演绎法，求卡塔兰数

直接利用公式进行计算：c(i+1)=c(i)(2(2n+1)/(n+2));

class Solution {
public:
    int numTrees(int n) {
        if(n<=1) return n;
        int c=1;
        for(int i=1;i<n;i++){
            long a=long(c)*long(4*i+2);
            long b=i+2;
            c=a/b;
        }
        return c;
    }
};