R语言与概率统计(三) 多元统计分析（下）广义线性回归

广义线性回归

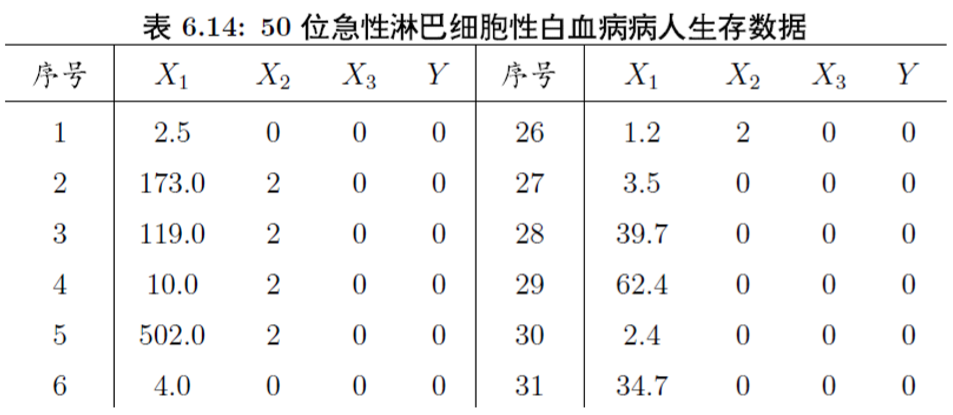
> life<-data.frame(
+   X1=c(2.5, 173, 119, 10, 502, 4, 14.4, 2, 40, 6.6,
+        21.4, 2.8, 2.5, 6, 3.5, 62.2, 10.8, 21.6, 2, 3.4,
+        5.1, 2.4, 1.7, 1.1, 12.8, 1.2, 3.5, 39.7, 62.4, 2.4,
+        34.7, 28.4, 0.9, 30.6, 5.8, 6.1, 2.7, 4.7, 128, 35,
+        2, 8.5, 2, 2, 4.3, 244.8, 4, 5.1, 32, 1.4),
+   X2=rep(c(0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2,
+            0, 2, 0, 2, 0, 2, 0),
+          c(1, 4, 2, 2, 1, 1, 8, 1, 5, 1, 5, 1, 1, 1, 2, 1,
+            1, 1, 3, 1, 2, 1, 4)),
+   X3=rep(c(0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1),
+          c(6, 1, 3, 1, 3, 1, 1, 5, 1, 3, 7, 1, 1, 3, 1, 1, 2, 9)),
+   Y=rep(c(0,  1,   0,  1), c(15, 10, 15, 10))
+ )
> glm.sol<-glm(Y~X1+X2+X3, family=binomial, data=life)
> summary(glm.sol)

Call:
glm(formula = Y ~ X1 + X2 + X3, family = binomial, data = life)

Deviance Residuals:
    Min       1Q   Median       3Q      Max
-1.6960  -0.5842  -0.2828   0.7436   1.9292  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.696538   0.658635  -2.576 0.010000 **
X1           0.002326   0.005683   0.409 0.682308
X2          -0.792177   0.487262  -1.626 0.103998
X3           2.830373   0.793406   3.567 0.000361 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 67.301  on 49  degrees of freedom
Residual deviance: 46.567  on 46  degrees of freedom
AIC: 54.567

Number of Fisher Scoring iterations: 5

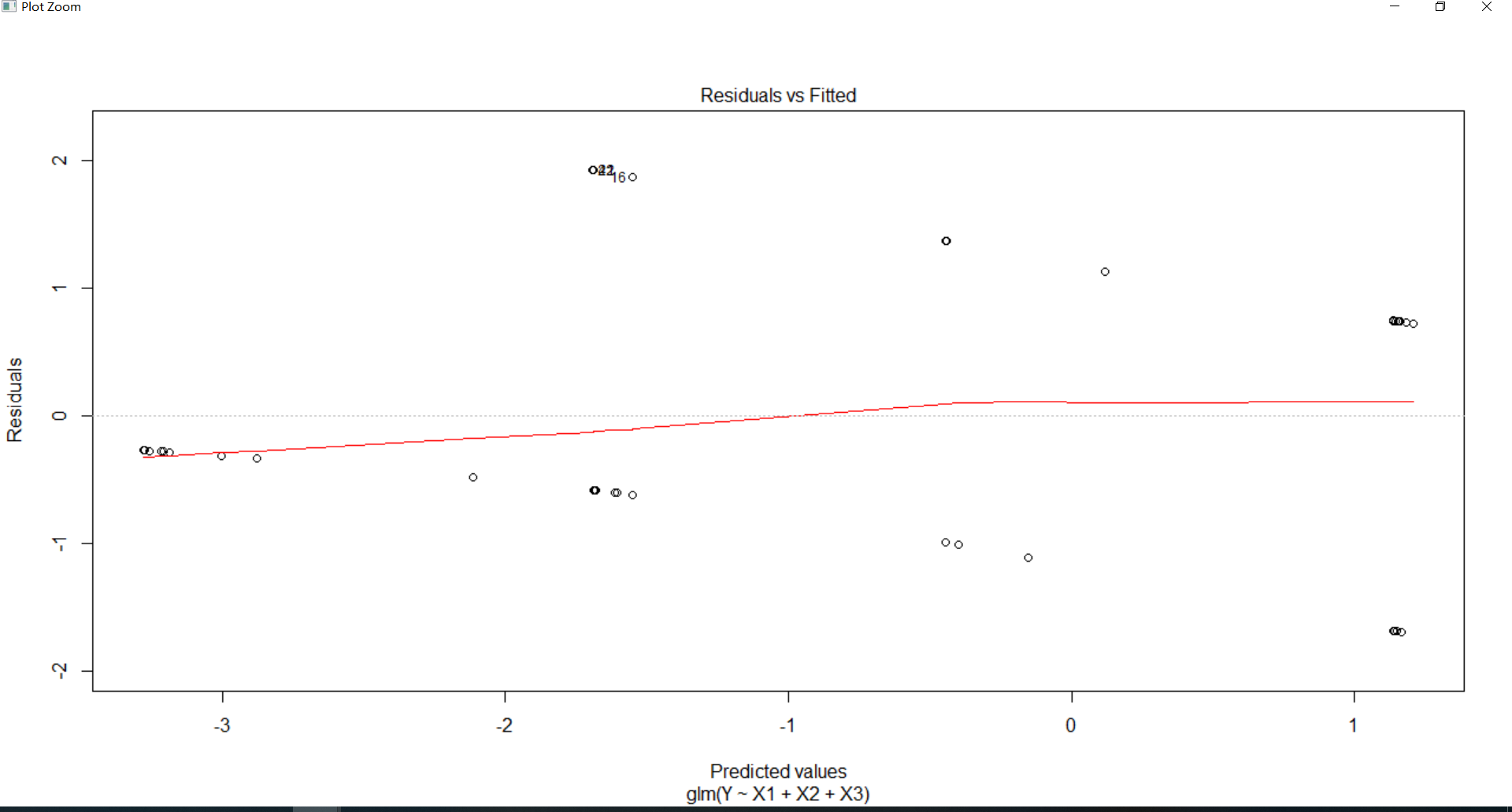
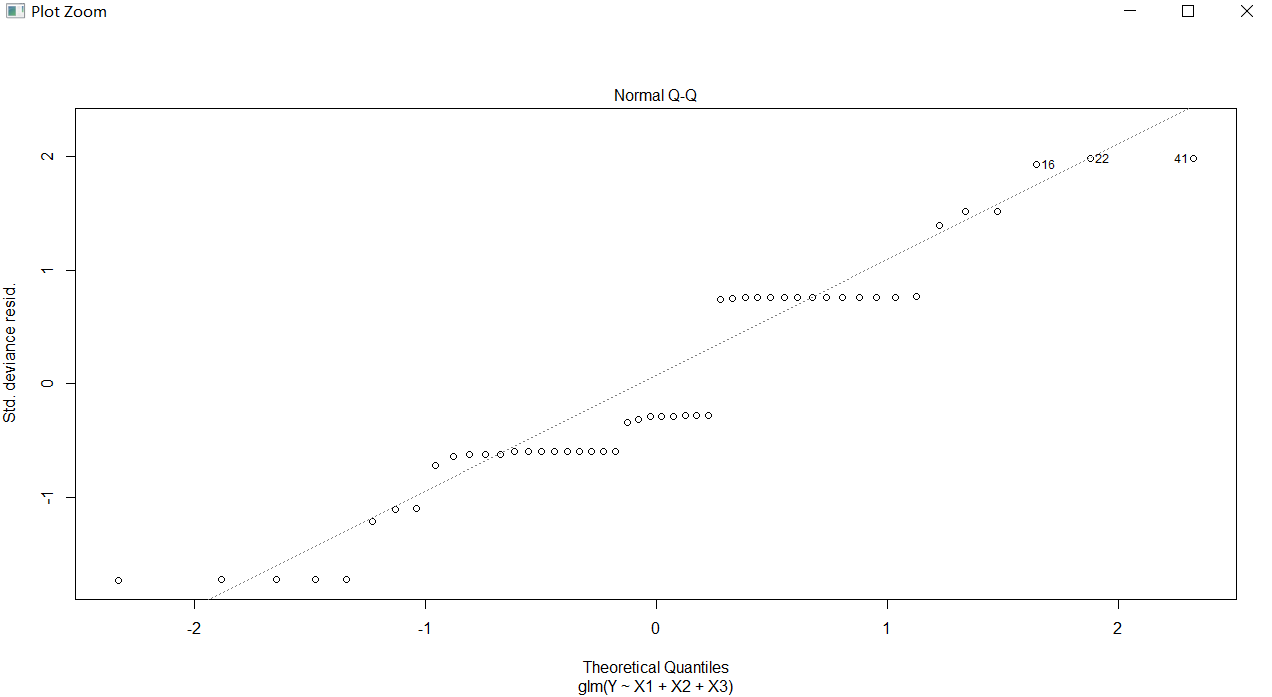
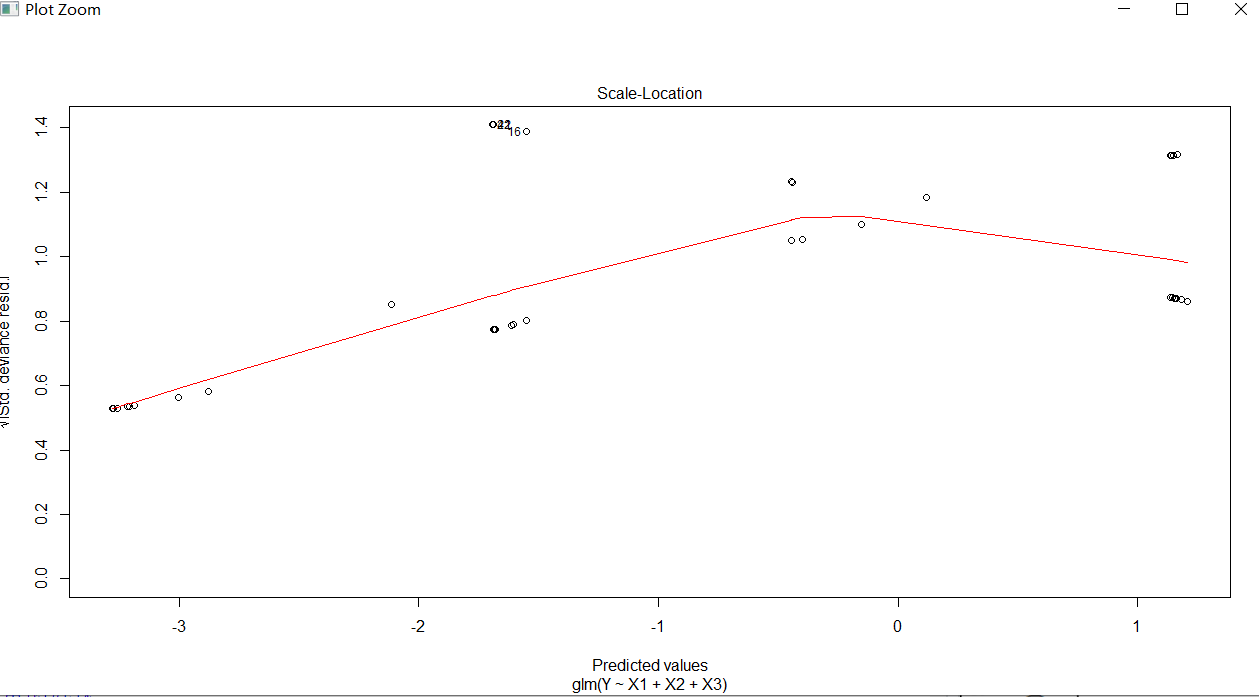
可见拟合的效果不好

> pre<-predict(glm.sol, data.frame(X1=5,X2=2,X3=0))
> p<-exp(pre)/(1+exp(pre));p#不接受治疗
         1
0.03664087
>
> pre<-predict(glm.sol, data.frame(X1=5,X2=2,X3=1))
> p<-exp(pre)/(1+exp(pre));p#接受治疗
        1
0.3920057
>
> step(glm.sol)
Start:  AIC=54.57
Y ~ X1 + X2 + X3

       Df Deviance    AIC
- X1    1   46.718 52.718
<none>      46.567 54.567
- X2    1   49.502 55.502
- X3    1   63.475 69.475

Step:  AIC=52.72
Y ~ X2 + X3

       Df Deviance    AIC
<none>      46.718 52.718
- X2    1   49.690 53.690
- X3    1   63.504 67.504

Call:  glm(formula = Y ~ X2 + X3, family = binomial, data = life)

Coefficients:
(Intercept)           X2           X3
     -1.642       -0.707        2.784  

Degrees of Freedom: 49 Total (i.e. Null);  47 Residual
Null Deviance:	    67.3
Residual Deviance: 46.72 	AIC: 52.72

> glm.new<-update(glm.sol, .~.-X1)
> summary(glm.new)

Call:
glm(formula = Y ~ X2 + X3, family = binomial, data = life)

Deviance Residuals:
    Min       1Q   Median       3Q      Max
-1.6849  -0.5949  -0.3033   0.7442   1.9073  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -1.6419     0.6381  -2.573 0.010082 *
X2           -0.7070     0.4282  -1.651 0.098750 .
X3            2.7844     0.7797   3.571 0.000355 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 67.301  on 49  degrees of freedom
Residual deviance: 46.718  on 47  degrees of freedom
AIC: 52.718

Number of Fisher Scoring iterations: 5

>
> pre<-predict(glm.sol, data.frame(X1=5,X2=2,X3=0))
> p<-exp(pre)/(1+exp(pre));p#不接受治疗
         1
0.03664087
>
> pre<-predict(glm.sol, data.frame(X1=5,X2=2,X3=1))
> p<-exp(pre)/(1+exp(pre));p#接受治疗
        1
0.3920057

#####再来看一个类似的问题
install.packages('AER')
data(Affairs,package='AER')#婚外情数据，包括9个变量，婚外斯通频率，性别，婚龄等。
summary(Affairs)
table(Affairs$affairs)
#我们感兴趣的是是否有过婚外情所以做如下处理
Affairs$ynaffair[Affairs$affairs>0]<-1
Affairs$ynaffair[Affairs$affairs==0]<-0
Affairs$ynaffair<-factor(Affairs$ynaffair,levels=c(0,1),labels=c('NO','YES'))
table(Affairs$ynaffair)
#接下来做逻辑回归
fit.full=glm(ynaffair~.-affairs,data=Affairs,family=binomial())
summary(fit.full)
#除掉较大p值所对应的变量，如性别，是否有孩子、学历和职业在做一次分析
fit.reduced=glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family=binomial())
summary(fit.reduced)

AIC(fit.full,fit.reduced)#模型比较

#系数解释
exp(coef(fit.reduced))