The Preliminary Contest for ICPC Asia Nanjing 2019 B. super_log （广义欧拉降幂）

In Complexity theory, some functions are nearly O(1)O(1), but it is greater then O(1)O(1). For example, the complexity of a typical disjoint set is O(nα(n))O(n**α(n)). Here α(n)α(n) is Inverse Ackermann Function, which growth speed is very slow. So in practical application, we often assume α(n) \le 4α(n)≤4.

However O(α(n))O(α(n)) is greater than O(1)O(1), that means if nn is large enough, α(n)α(n) can greater than any constant value.

Now your task is let another slowly function loglog∗ xx* reach a constant value bb. Here loglog∗ is iterated logarithm function, it means “the number of times the logarithm function iteratively applied on xx* before the result is less than logarithm base aa”.

Formally, consider a iterated logarithm function log_{a}^loga*∗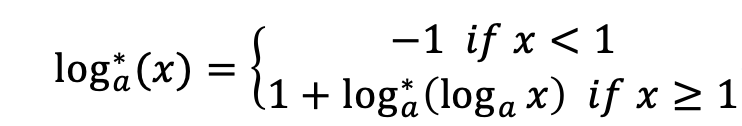

Find the minimum positive integer argument xx, let log_{a}^* (x) \ge blog**a∗(x)≥b. The answer may be very large, so just print the result xx after mod mm.

Input

The first line of the input is a single integer T(T\le 300)T(T≤300) indicating the number of test cases.

Each of the following lines contains 33 integers aa , bb and mm.

1 \le a \le 10000001≤a≤1000000

0 \le b \le 10000000≤b≤1000000

1 \le m \le 10000001≤m≤1000000

Note that if a==1, we consider the minimum number x is 1.

Output

For each test case, output xx mod mm in a single line.

Hint

In the 4-th4−t**h query, a=3a=3 and b=2b=2. Then log_{3}^* (27) = 1+ log_{3}^* (3) = 2 + log_{3}^* (1)=3+(-1)=2 \ge blog3∗(27)=1+log3∗(3)=2+log3∗(1)=3+(−1)=2≥b, so the output is 2727 mod 16 = 1116=11.

样例输入复制

5
2 0 3
3 1 2
3 1 100
3 2 16
5 3 233

样例输出复制

1
1
3
11
223

本题为 CF-906D 题目的更改版，请进我这篇博客学习对应题目：

https://www.cnblogs.com/qieqiemin/p/11478970.html

本题只需要改一下读入，加一个对幂次为０的特判即可通过。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
ll mod(ll x, ll m)
{
    return x >= m ? x % m + m : x;
}
ll powmod(ll a, ll b, ll MOD)
{
    ll ans = 1;
    while (b)
    {
        if (b % 2)
            ans = mod(ans * a, MOD);
        // ans = ans * a % MOD;
        // a = a * a % MOD;
        a = mod(a * a, MOD);
        b /= 2;
    }
    return ans;
}

ll m;
int n;
int q;
ll a;
map<ll, ll> vis;
ll euler(ll n) { //log(n)时间内求一个数的欧拉值
    if (vis.count(n))
    {
        return vis[n];
    }
    ll ans = n;
    for (ll i = 2; i * i <= n; i++) {
        if (n % i == 0)
        {
            ans -= ans / i;
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1) ans -= ans / n;
    vis[n] = ans;
    return ans;
}

ll solve(int l, int r, ll m)
{
    if (l == r || m == 1)
        return mod(a, m);
    return powmod(a, solve(l + 1, r, euler(m)), m);
}
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    scanf("%d", &q);
    int l, r;
    while (q--)
    {
        scanf("%d %d %lld", &a, &r, &m);
        if (r == 0)
        {
            printf("%lld\n", 1 % m );
            continue;
        }
        printf("%lld\n", solve(1, r, m) % m);
    }

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}