广义线性模型(logistic和softmax)
再谈广义线性模型之前,先来看一下普通线性模型:
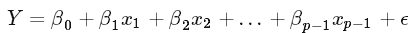
普通线性模型的假设主要有以下几点:
1.响应变量Y和误差项ϵ正态性:响应变量Y和误差项ϵ服从正态分布,且ϵ是一个白噪声过程,因而具有零均值,同方差的特性。
2.预测量xi和未知参数βi的非随机性:预测量xi具有非随机性、可测且不存在测量误差;未知参数βi认为是未知但不具随机性的常数,值得注意的是运用最小二乘法或极大似然法解出的未知参数的估计值β^i则具有正态性。
广义线性模型(generalized linear model)正是在普通线性模型的基础上,将上述四点模型假设进行推广而得出的应用范围更广,更具实用性的回归模型。此模式假设实验者所量测的随机变量的分布函数与实验中系统性效应(即非随机的效应)可经由一链结函数(link function)建立起可资解释其相关性的函数。响应变量的分布推广至指数分散族(exponential dispersion family):比如正态分布、泊松分布、二项分布、负二项分布、伽玛分布、逆高斯分布。
指数分布族
指数分布族(exponential dispersion family)实质上是对一类具有以下形式的概率密度函数或具有此类密度函数的分布的总括:
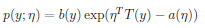
其中η成为分布的自然参数(natural parameter),T(y)成为充分统计,对于很多分类问题,这个值就是y,固定T,a,b,形成了一个参数是η的函数簇。
我们把伯努力分布写成:
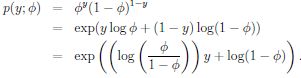
在这里自然参数η就是 。
。
以二分类为例,预测值y是二值的{1,0},假设给定x和参数,y的概率分布服从伯努利分布(对应构建GLM的第一条假设)。由上面高斯分布和指数家族分布的对应关系可知。
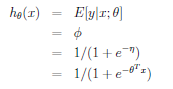
可以从GLM这种角度理解为什么logistic regression的公式是这个形式~
Logistic回归可以解决二元分类问题,但是对于多元分类,就需要使用Softmax回归来解决,比如对于邮件不是仅仅分为spam和not-spam,而是分为spam,personal,work
所以数据的分布也变成多项分布(multinomial distribution),是二项分布的推广
与上面不同的是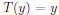 不再成立,取而代之的是
不再成立,取而代之的是
Softmax的指数分布族如下所示:

虽然看着挺复杂,但如果理解了logistic的相应函数,要看懂这个应该没问题。
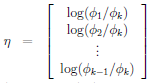
我们的目标是要取出其中的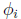 :
:
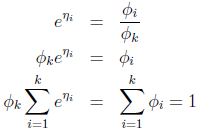
根据上述公式推导出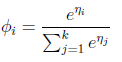 。
。
广义线性模型(logistic和softmax)的更多相关文章
- 机器学习 —— 基础整理(五)线性回归;二项Logistic回归;Softmax回归及其梯度推导;广义线性模型
本文简单整理了以下内容: (一)线性回归 (二)二分类:二项Logistic回归 (三)多分类:Softmax回归 (四)广义线性模型 闲话:二项Logistic回归是我去年入门机器学习时学的第一个模 ...
- 广义线性模型------逻辑回归和softmax回归
1.广义线性模型 2.逻辑回归 3.softmax回归
- Stanford大学机器学习公开课(四):牛顿法、指数分布族、广义线性模型
(一)牛顿法解最大似然估计 牛顿方法(Newton's Method)与梯度下降(Gradient Descent)方法的功能一样,都是对解空间进行搜索的方法.其基本思想如下: 对于一个函数f(x), ...
- 广义线性模型 GLM
Logistic Regression 同 Liner Regression 均属于广义线性模型,Liner Regression 假设 $y|x ; \theta$ 服从 Gaussian 分布,而 ...
- Logistic 与 softmax
之前写的一篇感觉太 Naive ,这里重新写一篇作为总结.Logistic 与 Softmax 都是一种概率判别模型(PRML p203),Softmax 通常用在 Neural Network 里最 ...
- 广义线性模型(Generalized Linear Models)
在线性回归问题中,我们假设,而在分类问题中,我们假设,它们都是广义线性模型的例子,而广义线性模型就是把自变量的线性预测函数当作因变量的估计值.很多模型都是基于广义线性模型的,例如,传统的线性回归模型, ...
- 斯坦福CS229机器学习课程笔记 part3:广义线性模型 Greneralized Linear Models (GLMs)
指数分布族 The exponential family 因为广义线性模型是围绕指数分布族的.大多数常用分布都属于指数分布族,服从指数分布族的条件是概率分布可以写成如下形式:η 被称作自然参数(nat ...
- 广义线性模型(GLM, Generalized Linear Model)
引言:通过高斯模型得到最小二乘法(线性回归),即: 通过伯努利模型得到逻辑回归,即: 这些模型都可以通过广义线性模型得到.广义线性模型是把自变量的线性预测函数当作因变量的估计值.在 ...
- SPSS数据分析—广义线性模型
我们前面介绍的一般线性模型.Logistic回归模型.对数线性模型.Poisson回归模型等,实际上均属于广义线性模型的范畴,广义 线性模型包含的范围非常广泛,原因在于其对于因变量.因变量的概率分布等 ...
随机推荐
- 打印 pmic register value
打印 PMIC register value 方式有二種, 一種是使用 adb shell cat pmic register 一種是直接在 code 裡 call dump pmic registe ...
- Tabular DataStream protocol 协议
Tabular DataStream protocol 协议 Freetds 创建过程 https://wenku.baidu.com/view/2076cbfaaef8941ea76e0576.ht ...
- python 使用headless chrome滚动截图
from selenium import webdriver from selenium.webdriver.chrome.options import Options import util chr ...
- java多线程以及Android多线程
Java 多线程 线程和进程的区别 线程和进程的本质:由CPU进行调度的并发式执行任务,多个任务被快速轮换执行,使得宏观上具有多个线程或者进程同时执行的效果. 进程:在操作系统来说,一个运行的程序或者 ...
- clearcase command (windows 常用的几个)
command 1. setview 指定某个view你可以操作,否则你将看不到文件,ls,cd 等其它命令无效 setview viewname 2. rename branch type na ...
- apache加入chkconfig
#First Step: cp /usr/local/apache2/bin/apachectl /etc/init.d/httpd #Second Step: vim /etc/init.d/htt ...
- Winfrom窗体间传值
1.通过tag属性传输,tag属性是存储与空间密切相关的数据.比如登陆界面的数据传输给主界面. 子窗体 ...
- Cent os FTP配置
原文:http://www.aicoffees.com/itshare/412261137.html
- java - 线程1打印1-10,当线程打印到5后,线程2打印“hello”,然后线程1继续打印
public class T { private static int a =1;//1代表线程1 2线程2 public static void main(String[] args) { fina ...
- django开发项目实例3--用session是实现简单的登陆、验证登陆和注销功能
如果你的网页不是纯阅读型的,那么你很有可能希望在用户打开某些界面的时候需要验证用户是否登陆的信息, 虽然django里面有自带的一些user的类,但我看不懂,并且自己实现也不是很难,下面和大家分享一下 ...
