最短路径-Dijkstra算法与Floyd算法

一、最短路径

　　①在非网图中，最短路径是指两顶点之间经历的边数最少的路径。

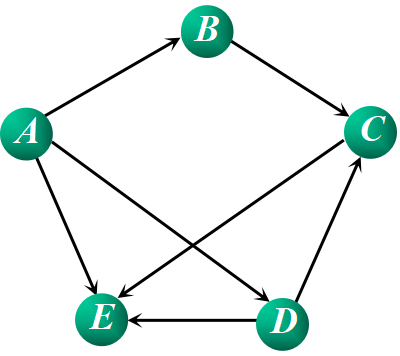
AE：1    ADE：2   ADCE：3   ABCE：3

　　②在网图中，最短路径是指两顶点之间经历的边上权值之和最短的路径。

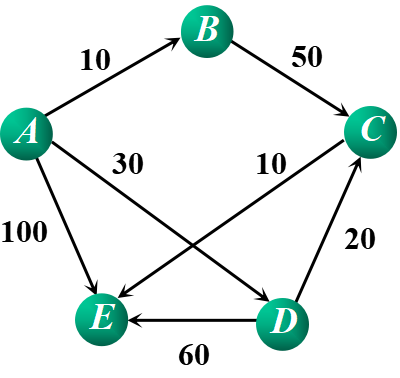
AE：100   ADE：90   ADCE：60   ABCE：70

　　③单源点最短路径问题

　　问题描述：给定带权有向图G＝(V, E)和源点v∈V，求从v到G中其余各顶点的最短路径。

　　应用实例——计算机网络传输的问题：怎样找到一种最经济的方式，从一台计算机向网上所有其它计算机发送一条消息。

　　④每一对顶点之间的最短路径

　　问题描述：给定带权有向图G＝(V, E)，对任意顶点vi,vj∈V（i≠j），求顶点vi到顶点vj的最短路径。

　　解决办法1：每次以一个顶点为源点，调用Dijkstra算法n次。显然，时间复杂度为O(n3)。 解决办法2：弗洛伊德提出的求每一对顶点之间的最短路径算法——Floyd算法，其时间复杂度也是O(n3)，但形式上要简单些。

二、Dijkstra算法

　　①基本思想：设置一个集合S存放已经找到最短路径的顶点，S的初始状态只包含源点v，对vi∈V-S，假设从源点v到vi的有向边为最短路径。以后每求得一条最短路径v, …, vk，就将vk加入集合S中，并将路径v, …, vk , vi与原来的假设相比较，取路径长度较小者为最短路径。重复上述过程，直到集合V中全部顶点加入到集合S中。

　　②设计数据结构 :

　　1、图的存储结构：带权的邻接矩阵存储结构 。

　　2、数组dist[n]：每个分量dist[i]表示当前所找到的从始点v到终点vi的最短路径的长度。初态为：若从v到vi有弧，则dist[i]为弧上权值；否则置dist[i]为∞。

　　3、数组path[n]：path[i]是一个字符串，表示当前所找到的从始点v到终点vi的最短路径。初态为：若从v到vi有弧，则path[i]为vvi；否则置path[i]空串。

　　4、数组s[n]：存放源点和已经生成的终点，其初态为只有一个源点v。

　　③Dijkstra算法——伪代码

 . 初始化数组dist、path和s；
 . while (s中的元素个数<n)
      2.1 在dist[n]中求最小值，其下标为k；
      2.2 输出dist[j]和path[j]；
      2.3 修改数组dist和path；
      2.4 将顶点vk添加到数组s中；

　　④C++代码实现

 #include<iostream>
 #include<fstream>
 #include<string>
 using  namespace std;
 #define MaxSize  10
 #define MAXCOST 10000
 // 图的结构
 template<class T>
 struct Graph
 {
     T vertex[MaxSize];// 存放图中顶点的数组
     int arc[MaxSize][MaxSize];// 存放图中边的数组
     int vertexNum, arcNum;// 图中顶点数和边数
 };
 // 最短路径Dijkstra算法
 void Dijkstra(Graph<string> G,int v)
 {
     int dist[MaxSize];//  i到j的路径长度
     string path[MaxSize];// 路径的串
     int s[MaxSize];// 已找到最短路径的点的集合
     bool Final[MaxSize];//Final[w]=1表示求得顶点V0至Vw的最短路径
     // 初始化dist\path
     for (int i = ; i < G.vertexNum; i++)
     {
         Final[i] = false;
         dist[i] = G.arc[v][i];
         if (dist[i] != MAXCOST)
             path[i] = G.vertex[v] + G.vertex[i];
         else
             path[i] = " ";
     }
     s[] = v; // 初始化s
     Final[v] = true;
     int num = ;
     while (num < G.vertexNum)
     {
         // 在dist中查找最小值元素
         int k = ,min= MAXCOST;
         for (int i = ; i < G.vertexNum; i++)
         {
             if (i == v)continue;
             if (!Final[i] && dist[i] < min)
             {
                 k = i;
                 min = dist[i];
             }
         }
         cout << dist[k]<<path[k]<<endl;
         s[num++] = k;// 将新生成的结点加入集合s
         Final[k] = true;
         // 修改dist和path数组
         for (int i = ; i < G.vertexNum; i++)
         {
             if (!Final[i]&&dist[i] > dist[k] + G.arc[k][i])
             {
                 dist[i] = dist[k] + G.arc[k][i];
                 path[i] = path[k] + G.vertex[i];
             }
         }
     }
 }
 int main()
 {
     // 新建图
     Graph<string> G;
     string temp[]= { "v0","v1","v2","v3","v4" };
     /*int length = sizeof(temp) / sizeof(temp[0]);
     G.vertexNum = length;
     G.arcNum = 7;*/
     ifstream in("input.txt");
     in >> G.vertexNum >> G.arcNum;
     // 初始化图的顶点信息
     for (int i = ; i < G.vertexNum; i++)
     {
         G.vertex[i] = temp[i];
     }
     //初始化图G的边权值
     for (int i =; i <G.vertexNum; i++)
     {
         for (int j = ; j <G.vertexNum; j++)
         {
             G.arc[i][j] = MAXCOST;
         }
     }
     for (int i = ; i < G.arcNum; i++)
     {
         int m, n,cost;
         in >> m >> n >> cost;
         G.arc[m][n] = cost;
     }
     Dijkstra(G, );
     system("pause");
     return ;
 }

// input.txt
1  

三、Floyd算法

　　①基本思想：对于从vi到vj的弧，进行n次试探：首先考虑路径vi,v0,vj是否存在，如果存在，则比较vi,vj和vi,v0,vj的路径长度，取较短者为从vi到vj的中间顶点的序号不大于0的最短路径。在路径上再增加一个顶点v1，依此类推，在经过n次比较后，最后求得的必是从顶点vi到顶点vj的最短路径。

　　②设计数据结构

　　1、图的存储结构：带权的邻接矩阵存储结构  。

　　2、数组dist[n][n]：存放在迭代过程中求得的最短路径长度。迭代公式：

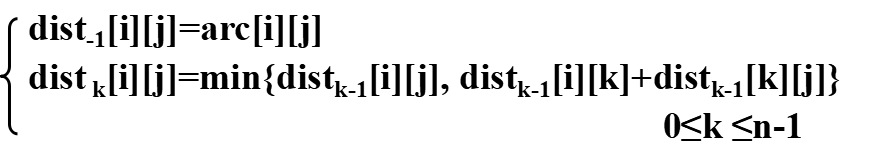
　　3、数组path[n][n]：存放从vi到vj的最短路径，初始为path[i][j]="vivj"。

　　③C++代码实现

 #include<iostream>
 #include<fstream>
 #include<string>
 using  namespace std;
 #define MaxSize  10
 #define MAXCOST 10000
 int dist[MaxSize][MaxSize];// 存放在迭代过程中求得的最短路径
 string path[MaxSize][MaxSize];// vi到vj的最短路径
 // 图的结构
 template<class T>
 struct Graph
 {
     T vertex[MaxSize];// 存放图中顶点的数组
     int arc[MaxSize][MaxSize];// 存放图中边的数组
     int vertexNum, arcNum;// 图中顶点数和边数
 };
 void Floyd(Graph<string> G)
 {
     // 初始化
     for(int i=;i<G.vertexNum;i++)
         for (int j = ; j < G.vertexNum; j++)
         {
             if (i == j) { dist[i][j] = ; path[i][j] = ""; }
             dist[i][j] = G.arc[i][j];
             if (dist[i][j] != MAXCOST)
                 path[i][j] = G.vertex[i] + G.vertex[j];
             else
                 path[i][j] = " ";
         }
     // 进行n次迭代
     for(int k=;k<G.vertexNum;k++)
         for(int i=;i<G.vertexNum;i++)
             for (int j = ; j < G.vertexNum; j++)
                 if (dist[i][k] + dist[k][j] < dist[i][j])
                 {
                     dist[i][j] = dist[i][k] + dist[k][j];
                     path[i][j] = path[i][k] + path[k][j];
                 }
 }
 int main()
 {
     int i, j, cost;
     Graph<string> G;// 存放图的信息
     ifstream in("input.txt");
     in >> G.vertexNum >> G.arcNum;
     string temp[] = { "a","b","c" };
     // 初始化图的顶点信息
     for (int i = ; i < G.vertexNum; i++)
     {
         G.vertex[i] = temp[i];
     }
     //初始化图G
     for (i = ; i < G.vertexNum; i++)
     {
         for (j = ; j < G.vertexNum; j++)
         {
             G.arc[i][j] = MAXCOST;
         }
     }
     //构建图G
     for (int k = ; k <G.arcNum; k++)
     {
         in >> i >> j >> cost;
         G.arc[i][j] = cost;
     }
     Floyd(G);
     for (i = ; i < G.vertexNum; i++)
     {
         for (j = ; j < G.vertexNum; j++)
         {
             if (i != j)
             {
                 cout << "顶点" << i << "到顶点" << j << "的最短路径长度为" << dist[i][j] << endl;
                 cout << "具体路径为:" << path[i][j] << endl;
             }
         }
     }
     system("pause");
     return ;
 }

// input.txt

参考文献：

[1]王红梅, 胡明, 王涛. 数据结构(C++版)[M]. 北京：清华大学出版社。