LeetCode-1：Two Sum

【Problem：1-Two Sum】

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

【Example】

Given nums = [, , , ], target = ,

Because nums[] + nums[] =  +  = ,
return [, ].

【Solution】

1）-----------Submission Status ：Time Limit Exceeded

Time complexity：O(n^2)2​​).

【Python】
import time
class Solution(object):
    def twoSum(self,nums,target):
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                if nums[i]+nums[j]==target:
                    return i,j

start = time.clock()
test=Solution()
nums=[1,2,3,4,5,55,26,25,36,211,200,300,258,459]
target=8
print("The indices are :",test.twoSum(nums,target))

end = time.clock()
c=end-start
print("Runtime is ：",c)

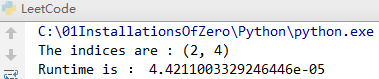
可是 Java 的这个，Time complexity 也是O(n^2)2 ，却可以 AC？？

【Java】
public int[] twoSum(int[] nums, int target) {
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] == target - nums[i]) {
                return new int[] { i, j };
            }
        }
    }
    throw new IllegalArgumentException("No two sum solution");
}

2）两个方法做个对比：（Python 语言）

#----
class Solution(object):
    # Method 1 : O(n_2)
    def twoSum1(self,nums,target):
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                if nums[i]+nums[j]==target:
                    return i,j

    # Method 2 : O(n)
    def twoSum2(self, nums, target):
            if len(nums) <= 1:
                return False
            buff_dict = {}
            for i in range(len(nums)):
                if nums[i] in buff_dict:
                    return [buff_dict[nums[i]], i]
                else:
                    buff_dict[target - nums[i]] = i

test=Solution()
nums=[1,2,3,4,5,55,26,25,36]
target=8

start1 = time.clock()
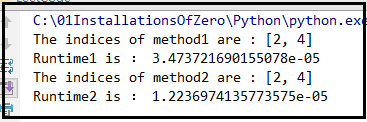
print("The indices of method1 are :",test.twoSum2(nums,target))
end1 = time.clock()
t1=end1-start1
print("Runtime1 is ：",t1)

start2 = time.clock()
print("The indices of method2 are :",test.twoSum2(nums,target))
end2 = time.clock()
t2=end2-start2
print("Runtime2 is ：",t2)

结果是：

3）外加一个方法3 ，会比法2好些？（亦可AC）

#----
class Solution(object):
    # Method 1 : O(n_2)
    def twoSum1(self,nums,target):
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                if nums[i]+nums[j]==target:
                    return i,j

    # Method 2 : O(n)
    def twoSum2(self, nums, target):
            if len(nums) <= 1:
                return False
            buff_dict = {}
            for i in range(len(nums)):
                if nums[i] in buff_dict:
                    return [buff_dict[nums[i]], i]
                else:
                    buff_dict[target - nums[i]] = i

    def twoSum3(self, num, target):
            tmp_num = {}
            for i in range(len(num)):
                if target - num[i] in tmp_num:
                    # here do not need to deal with the condition i = target-i
                    return (tmp_num[target-num[i]], i)
                else:
                    tmp_num[num[i]] = i
            return (-1, -1)

test=Solution()
nums=[1,2,3,4,5,55,26,25,36]
target=8

start1 = time.clock()
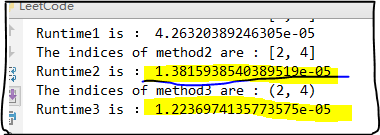
print("The indices of method1 are :",test.twoSum2(nums,target))
end1 = time.clock()
t1=end1-start1
print("Runtime1 is ：",t1)

start2 = time.clock()
print("The indices of method2 are :",test.twoSum2(nums,target))
end2 = time.clock()
t2=end2-start2
print("Runtime2 is ：",t2)

start3 = time.clock()
print("The indices of method3 are :",test.twoSum3(nums,target))
end3 = time.clock()
t3=end3-start3
print("Runtime3 is ：",t3)

结果是：