Gabor变换、Gabor滤波器

D.Gabor 1946年提出

窗口Fourier变换，为了由信号的Fourier变换提取局部信息，引入了时间局部化的窗函数。

由于窗口Fourier变换只依赖于部分时间的信号，所以，现在窗口Fourier变换又称为短时Fourier变换，这个变换又称为Gabor变换。

1) Gabor优点

Gabor小波与人类视觉系统中简单细胞的视觉刺激响应非常相似。它在提取目标的局部空间和频率域信息方面具有良好的特性。虽然Gabor小波本身并不能构成正交基，但在特定参数下可构成紧框架。Gabor小波对于图像的边缘敏感，能够提供良好的方向选择和尺度选择特性，而且对于光照变化不敏感,能够提供对光照变化良好的适应性。上述特点使Gabor小波被广泛应用于视觉信息理解。

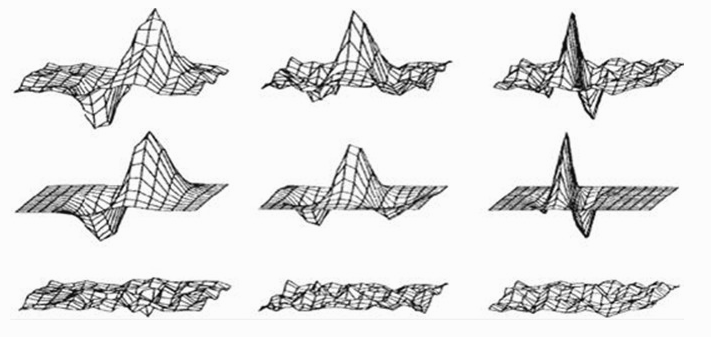
Gabor滤波器和脊椎动物视觉皮层感受野响应的比较：第一行代表脊椎动物的视觉皮层感受野，第二行是Gabor滤波器，第三行是两者的残差。可见两者相差极小。Gabor滤波器的这一性质，使得其在视觉领域中经常被用来作图像的预处理。

2) Gabor定义

① 具体窗函数――Gaussaion的 Gabor变换定义式

Gabor变换的基本思想：把信号划分成许多小的时间间隔，用傅里叶变换分析每一个时间间隔，以便确定信号在该时间间隔存在的频率。其处理方法是对f(t)加一个滑动窗，再作傅里叶变换。

② 窗口的宽高关系

经理论推导可以得出：高斯窗函数条件下的窗口宽度与高度，且积为一固定值。

3) 离散Gabor变换的一般求法

① 首先选取核函数

可根据实际需要选取适当的核函数。如，如高斯窗函数；

② 离散Gabor变换的表达式

4) Gabor变换的解析理论

对偶函数可以使计算更为简洁方便。

5) 适用条件

① 临界采样Gabor展开要求条件：TΩ=2π；

② 过采样展开要求条件：TΩ≤2π；

当TΩ＞2π时，欠采样Gabor展开，已证明会导致数值上的不稳定。

6) 应用

① 暂态信号检测

如果对信号波形有一定的先验知识且可以据此选取合适的基函数，可以用Gabor变换对信号作精确的检测统计计量。

② 图象分析与压缩

二维Gabor变换可以应用到图象分析与压缩中。

3. 二维Gabor滤波器

用Gabor 函数形成的二维Gabor 滤波器具有在空间域和频率域同时取得最优局部化的特性，因此能够很好地描述对应于空间频率(尺度)、空间位置及方向选择性的局部结构信息。

Gabor滤波器的频率和方向表示接近人类视觉系统对于频率和方向的表示，并且它们常备用于纹理表示和描述。

在图像处理领域，Gabor滤波器是一个用于边缘检测的线性滤波器。

在空域，一个2维的Gabor滤波器是一个正弦平面波和高斯核函数的乘积。

Gabor滤波器是自相似的，也就是说，所有Gabor滤波器都可以从一个母小波经过膨胀和旋转产生。

实际应用中，Gabor滤波器可以在频域的不同尺度，不同方向上提取相关特征。

Gabor滤波器的傅里叶变换：峰值响应在复正弦的空域频率(u0,v0)：

Gabor滤波器示意图，3种角度5种方向：

【链接】

转载自：Gabor学习笔记 - emouse - 博客园 http://www.cnblogs.com/emouse/p/3611256.html

纹理分割(一)Gabor滤波器学习 - Focusing on your own Mind :) －> 站在巨人的肩膀上 - CSDN博客 https://blog.csdn.net/u011534057/article/details/72896921

生成2维Gabor滤波器的matlab 代码：

http://blog.sina.com.cn/s/blog_80853788010103wx.html

http://blog.csdn.net/weixingstudio/article/details/7872764

Opencv实现：

http://www.cppblog.com/polly-yang/archive/2012/07/14/183327.aspx

【其他】

傅立叶变换、Gabor变换与小波变换 - chenaiyanmie的博客 - CSDN博客 https://blog.csdn.net/chenaiyanmie/article/details/80246108

Gabor滤波进行目标图像纹理特征的提取 - yangdashi888的博客 - CSDN博客 https://blog.csdn.net/yangdashi888/article/details/52766530

对于gabor变换和gabor小波变换理解与总结 - weixin_38698410的博客 - CSDN博客 https://blog.csdn.net/weixin_38698410/article/details/79122871

从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换 - 彬彬有礼的专栏 - CSDN博客 https://blog.csdn.net/jbb0523/article/details/42028587