【Udacity】误差原因——方差variance与偏差bias

• 偏差造成的误差-准确率和欠拟合
• 方差-精度和过拟合
• Sklearn代码
• 理解bias &variance

在模型预测中，模型可能出现的误差来自两个主要来源，即：因模型无法表示基本数据的复杂度而造成的偏差（bias），或者因模型对训练它所用的有限数据过度敏感而造成的方差（variance）。我们会对两者进行更详细的探讨。

一、偏差造成的误差-准确率和欠拟合

如前所述，如果模型具有足够的数据，但因不够复杂而无法捕捉基本关系，则会出现偏差。这样一来，模型一直会系统地错误表示数据，从而导致准确率降低。这种现象叫做__ 欠拟合（underfitting）__。

简单来说，如果模型不适当，就会出现偏差。举个例子：如果对象是按颜色和形状分类的，但模型只能按颜色来区分对象和将对象分类（模型过度简化），因而一直会错误地分类对象。

或者，我们可能有本质上是多项式的连续数据，但模型只能表示线性关系。在此情况下，我们向模型提供多少数据并不重要，因为模型根本无法表示其中的基本关系，我们需要更复杂的模型。

二、方差-精度和过拟合

在训练模型时，通常使用来自较大训练集的有限数量样本。如果利用随机选择的数据子集反复训练模型，可以预料它的预测结果会因提供给它的具体样本而异。在这里，方差（variance）用来测量预测结果对于任何给定的测试样本会出现多大的变化。

出现方差是正常的，但方差过高表明模型无法将其预测结果泛化到更多的数据。对训练集高度敏感也称为__ 过拟合（overfitting）__，而且通常出现在模型过于复杂或我们没有足够的数据支持它时。

通常，可以利用更多数据进行训练，以降低模型预测结果的方差并提高精度。如果没有更多的数据可以用于训练，还可以通过限制模型的复杂度来降低方差。

三、Sklearn代码

3.1 学习曲线 Learning_Curve

现在你理解了偏差和方差的概念，让我们学习一下如何辨别模型表现的好坏。sklearn中的学习曲线函数可以帮到我们。它可以让我们通过数据点来了解模型表现的好坏。

可以先引入这个模块

from sklearn.learning_curve import learning_curve # sklearn 0.17
from sklearn.model_selection import learning_curve # sklearn 0.18

文档中一个合理的实现是：

 learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)

这里estimator是我们正在用来预测的模型，例如它可以是GaussianNB()，X和y是特征和目标。cv是交叉验证生成器，例如KFold()，'n_jobs'是平行运算的参数，train_sizes是多少数量的训练数据用来生成曲线。

四、理解方差和偏差

一图顶万字

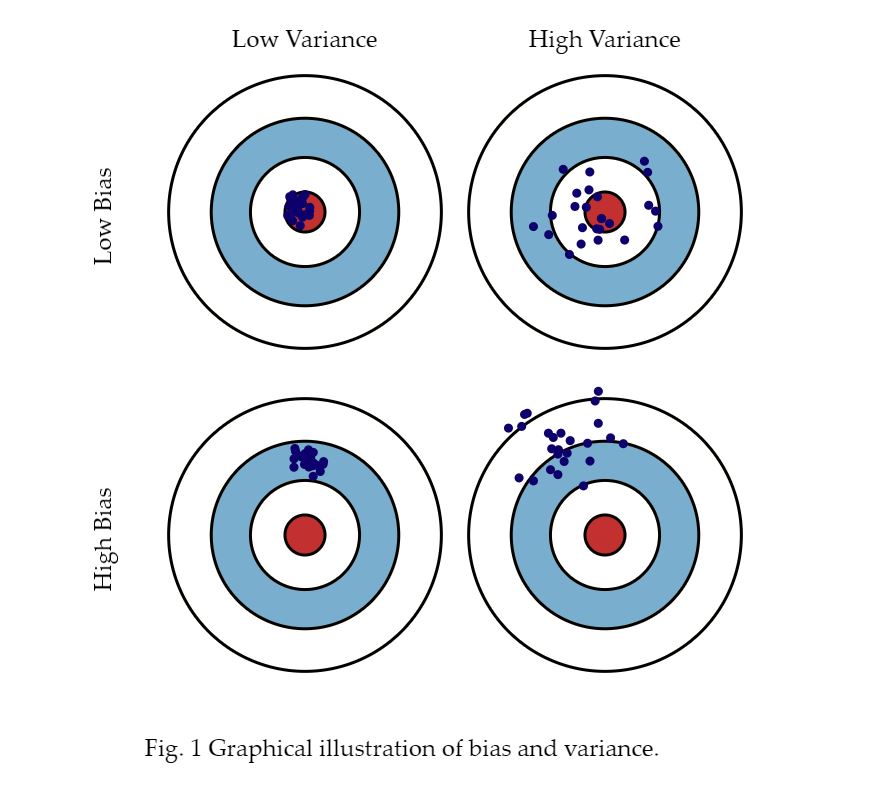
要详细了解偏差和方差，建议阅读 Scott Fortmann-Roe 撰写的这篇文章。