2115: [Wc2011] Xor （线性基+dfs）

2115: [Wc2011] Xor

Time Limit: 10 Sec  Memory Limit: 259 MB
Submit: 5714  Solved: 2420

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=2115

Description:

Input:

第一行包含两个整数N和 M， 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边，每行三个整数Si，Ti ，Di，表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。

Output:

仅包含一个整数，表示最大的XOR和（十进制结果）,注意输出后加换行回车。

Sample Input:

1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2

Sample Output:

6

Hint:

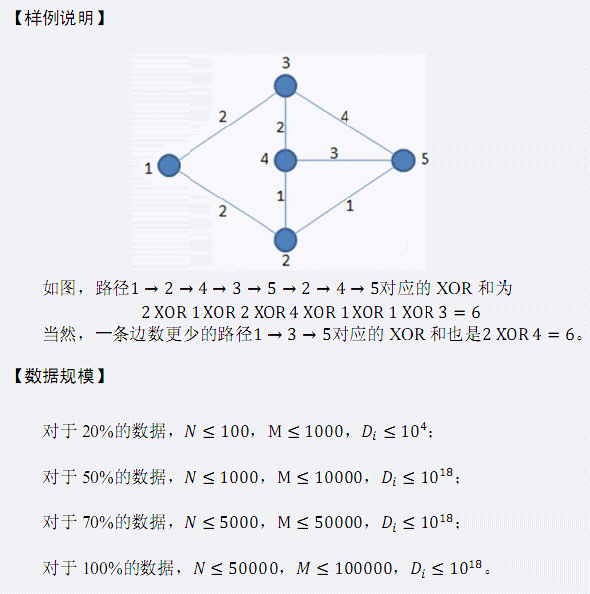
题解：

我感觉这个题是很巧妙的一个题，直接dfs搜路径是显然行不通的。

其实通过观察可以发现，最终的最大异或值所走的路径，一定是一条路径加上若干环形成的。

那么我们考虑通过一次dfs将所有环的异或和求出来，然后随便选择一条路径作为我们的起始路径，这里有两种情况：

1.环没在路径上，那么此时我们走的时候就是通过若干点到那个环，然后又从那若干点回来，最终对答案有贡献的就只有环的异或和；

2.环在路径上，此时我们将这个环与原路径异或一下，那么原路径与环重叠部分就会抵消，然后会形成一条新的更优的路径。

那么此时如果我们将环与路径的最大异或值找出来，最终也是一条路径和若干环，这时就考虑利用线性基来求异或最大值。

代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = ,M = ;
int n,m,tot,num;
int head[N],vis[N];
ll x[N],cir[N<<];
struct Edge{
    int u,v,next;
    ll w;
}e[M<<];
void adde(int u,int v,ll w){
    e[tot].v=v;e[tot].next=head[u];e[tot].w=w;head[u]=tot++;
}
void dfs(int u,int fa){
    vis[u]=;
    for(int i=head[u];i!=-;i=e[i].next){
        int v=e[i].v;
        if(v==fa) continue ;
        if(!vis[v]){
            x[v]=x[u]^e[i].w;
            dfs(v,u);
        }else{
            cir[++num]=x[v]^x[u]^e[i].w;
        }
    }
}
ll p[];
ll ans;
void xor_base(){
    for(int i=;i<=num;i++){
        for(ll j=;j>=;j--){
            if((1LL<<j)&cir[i]){
                if(!p[j]){
                    p[j]=cir[i];
                    break;
                }
                cir[i]^=p[j];
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(false);cin.tie();
    cin>>n>>m;
    memset(head,-,sizeof(head));tot=num=;
    for(int i=;i<=m;i++){
        int u,v;ll w;
        cin>>u>>v>>w;
        adde(u,v,w);adde(v,u,w);
    }
    dfs(,-);
    ans=x[n];
    xor_base();
    for(int i=;i>=;i--){
        ans=max(ans,ans^p[i]);
    }
    cout<<ans;
    return ;
}