C# 顺序高斯（Gauss）消去法计算一元多次方程组

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;

 namespace zblGauss1
 {
     class Program
     {
         static void Main(string[] args)
         {
             double[,] a = { { 8.1, 2.3, -1.5, 6.1 }, { 0.5, -6.23, 0.87, 2.3 }, { 2.5, 1.5, 10.2, 1.8 } };
             //double[,] a = { { 2, -1, 3, 1 }, { 4, 2, 5, 4 }, { 1, 2, 0, 7 } };
             int n = a.GetLength();//数组a的第一维长度，即行数,3
             double[] x = new double[n];//存放解的数组，初始值为0

             Gauss1(n, a, x);//调用Gauss1 方法计算用顺序高斯消去法计算一元多次方程组
             Console.WriteLine("方程的根为：");//输出方程组的根
             for (int i = ; i < n; i++)
             {
                 Console.Write("x{0}={1,10:F10}, ", i, x[i]);
             }
         }

         //利用顺序高斯Gauss消元法求一元多次线性方程组的解
         public static void Gauss1(int n, double[,] a, double[] x)//写了一个静态方法，方法可以在别的方法中直接调用，不必声明对象然后调用对象中的方法了
         {
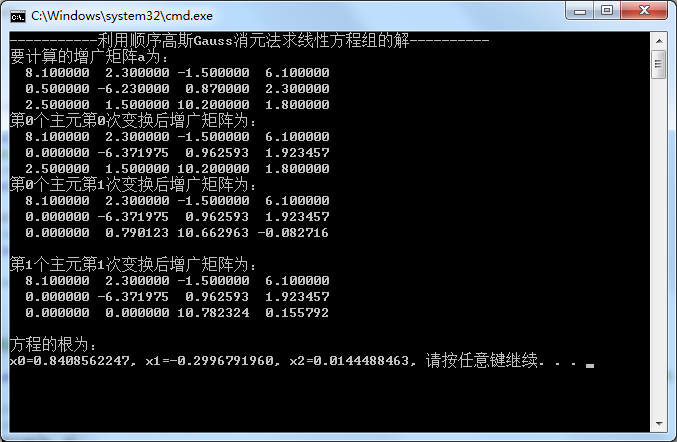
             Console.WriteLine("-----------利用顺序高斯Gauss消元法求线性方程组的解----------");
             Console.WriteLine("要计算的增广矩阵a为：");
             printArray(n, a);

             //消元过程
             for (int k = ; k < n - ; k++)//k=0 1 ，弄出来两个主元即可 ,两次大循环，此称为1层循环  ---主元---
             {
                 for (int i = k; i < n - ; i++)//每个大循环中   要对主元素下面所有元素变化为零,，  ---行---  ，i= 0 1 ，此称为2层循环
                 {
                     double m = a[i + , k] / a[k, k];//可能用到多次，在此将化零因子放入m中
                     for (int j = k; j <= n; j++) //2层循环中要对每行所有元素都做相同变化，   ---列---    ，  j=
                     {
                         a[i + , j] = a[i + , j] - m * a[k, j];//由于第一行第一列元素不用化零，故首先从i+1开始，同列所以后面都是j，k处为主元行处
                     }
                     Console.WriteLine("第{0}个主元第{1}次变换后增广矩阵为：", k, i);
                     printArray(n, a);
                 }
                 Console.WriteLine();
             }

             //回代过程
             for (int k = n - ; k >= ; k--) //k=2 1 0 从最后一行开始往前迭代
             {
                 double addResult = 0.0;//用于存放已知的未知数代入相应式子中之和，换一行计算时需要清零，故放在此处
                 for (int j = k; j < n - ; j++)//j=2   j 最大值为2，每行未知数可能不止一个，故需要遍历已知的未知数并代入
                 {
                     addResult = addResult + x[j + ] * a[k, j + ];//k代表计算的行，j+1代表的列，系数与解要对应，故都为 j+1
                 }
                 x[k] = (a[k, n] - addResult) / a[k, k];//本行的未知数用本行最右边数-本行已知未知数代入系数之差 再除以本未知数系数
             }

         }
         public static void printArray(int n, double[,] a)
         {
             for (int i = ; i < n; i++)
             {
                 for (int j = ; j <= n; j++)
                 {
                     Console.Write("{0,10:F6}", a[i, j]);
                 }
                 Console.WriteLine();
             }

         }
     }
 }

高斯消去法由消元和回代两个过程组成。消元就是对增广矩阵做有限次的初等行变换，使它的系数矩阵部分变为一个上三角矩阵。所用的初等行变换主要有两种：第一种，交换两行的位置；第二种，用一个数乘某一行加到另一行上。

经过n-1次消元后，原增广矩阵变为行阶梯矩阵。

高斯消去法分为顺序高斯消去法和列主元素消去法两种。

顺序高斯消去法：在消元过程中对增广矩阵只做前述的第二种初等行变换就形成了顺序Gauss消去法。

原创， 转载请注明出处，谢谢。